Ampere turn balance (MMF balance) in transformers

[gorlyu]

Hi all,
I have been battling this topic for one year now. Frequenctly revisiting it and trying to find a clear answer on the internet and in but without finding it. Could be that my knowledge level is too low. However, I'll give it a shot here.

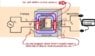
So what I have been learned is that during no-load of the transformer with high permeability cores there is perfect coupling from primary to secondary. I .e. the voltage ratio equals the turn ratio. When loading the transformer the secondary will produce an mmf that is balanced by the primary mmf with a small deviation in terms of magnetization current on the primary.

However, there is a leakage flux making up the series impedance. This leakage flux is imperfect coupling during load from primary to secondary and as I understand it, secondary to primary. I.e. both coils have their own associated leakage flux and therefore series impedance.

What bothers me is that this leakage flux is constituted in terms of a voltage drop or rise, and not loss of current. I know I'm wrong but I cannot understand why. My thinking is as follows:

- Let's say you produce a certain mmf in the primary coil but part of that mmf is the leakage flux, consequently the secondary coil cannot balance that leakage flux (because it is not linking the secondary) and hence there would an imbalance in terms of mmf.

There is something fundamental I'm missing here and I would appreciate clearing this out.Gorlyu

P.s.
A similar situation is for current transformers. They are designed for a certain current ratio between primary and secondary. That current ratio will not change when you increase the distance between the primary and CT-core? So there is no difference in that ratio if you have 3 cm diameter of a CT or 300 cm? Given that you introduce no additional disturbances.

 

[anorlunda]

It sounds like you are not asking how transformers behave, but rather the words used to describe it. Is that correct?

Are you looking for a mathematical answer or a verbal one?

Maxwells Equations are the tool to use to accurately calculate what happens with 3D fields. If you are thinking verbally, I can't help you.

There was a very long thread on PF about internal fluxes in transformers. More than 100 posts in that thread I think. I can't find the link but perhaps @jim hardy remembers it.

 

[gorlyu]

I'm more out after a verbal explanation rather than an equation based answer. A thread on internal fluxes seems like something that could be useful.

It is probably easy to make a simple illustrative question as well. I might give that a try later.

 

[anorlunda]

I think I found the thread https://www.physicsforums.com/threa...rs-across-the-ideal-transformer.819580/page-2

Pour yourself a cup of coffee and put your feet up to real all 359 posts in that thread.

 

[jim hardy]

It is probably easy to make a simple illustrative question as well. I might give that a try later.

Yes. Phrasing a question well often answers it .

That's the longest thread i remember. I can remember having other discussions. That Wikipedia model circuit works pretty well for a 'nuts and bolts' understanding.

old jim

 

[jim hardy]

see also

https://www.physicsforums.com/threads/inductance-and-capacitance-as-the-secondary-load.921831/
https://www.physicsforums.com/threa...ap-changing-transformers.932452/#post-5889911

 

[gorlyu]

Thanks to both of you. I've read the threads without becoming satisfied, however I'm slightly more happy of course.

I'll try to reformulate myself:

Wikipedia describes the relation between leakage inductance and transformer operation like this:

A transformer works because a magnetic circuit in the core which transfers energy couples its electric windings, which are inductors. A magnetic circuit is an electromagnet, a magnet that is magnetized only when electricity flows in its coil. But not all of the electric energy can be transferred to magnetic energy in the core (and not all of the magnetic energy in the core can be transferred back to another electric circuit) – some becomes a magnetic field in the air. The "wasted" energy in that magnetic field is called leakage flux. However, leakage flux is not lost in the same way as electrical energy which is dissipated in the form of heat. Leakage flux remains as part of the energy in the electric circuit. Its effect is to add some incremental "resistance"[Notes 1] to the flow of electricity in that circuit. That "resistance" is called leakage inductance.

My interpretation is like this:
For a transformer with a high permeability core: when the secondary is loaded it draws a current, that current is balanced by the primary. The two mmf:s cancels each other completely. However, some part of that mmf, for both the primary and secondary does give rise to an inductance in the transformer. This is what we call the leakage inductance. BUT, no flux generated by the mmf:s leaks in that way that transformer operation is affected. So it is not really leakage flux since we have perfect linkage. So what is it then?

And here comes my pedagogical attempt of formulating a question that will lead us forward:
Assuming you have a transformer that have no resistances in the coils and has a high permeability core of todays standards. When short-circuiting the secondary you measure a certain leakage inductance.

Question 1: do you agree that the mmfs of each coil are in perfect balance in this case (they cancel - except the magnetization current from the feeding side)?

Question 2: Let's say you replace that core with an ideal core with infinite permeability and no hysteresis or eddy losses. Without changing the coils. Will you still measure that leakage inductance?gorlyu

 

[sophiecentaur]

Question 2: Let's say you replace that core with an ideal core with infinite permeability and no hysteresis or eddy losses. Without changing the coils. Will you still measure that leakage inductance?

Wouldn't the leakage of flux approach zero so the leakage Impedance would then be zero? (No flux at all through the air)

What bothers me is that this leakage flux is constituted in terms of a voltage drop or rise, and not loss of current. I know I'm wrong but I cannot understand why.

The leakage Impedance is an 'Equivalent' circuit component. If you tried to model with a Shunt Admittance, I think it wouldn't model as having constant component values as the load current was varied. That wouldn't be useful. (All these Equivalent Components are only in our heads and used as a convenient model.)

 

[gorlyu]

Wouldn't the leakage of flux approach zero so the leakage Impedance would then be zero? (No flux at all through the air)

Hi,
Well. If it is like that, that means the leakage inductance is a result of imperfect core.

Would that not also mean that we would see that leakage inductance in the no-load condition for a real core?

 

[sophiecentaur]

Hi,
Well. If it is like that, that means the leakage inductance is a result of imperfect core.

Would that not also mean that we would see that leakage inductance in the no-load condition for a real core?

As it's in series, there would be nothing to see in the no load condition 'cos no current would be flowing. But I guess the non-induction resistance would be a current path so the V ratio might not the exactly the Turns ratio. But a transformer working a well below its design frequency would not be a realistic case.

 

[gorlyu]

As it's in series, there would be nothing to see in the no load condition 'cos no current would be flowing. But I guess the non-induction resistance would be a current path so the V ratio might not the exactly the Turns ratio. But a transformer working a well below its design frequency would not be a realistic case.

Ok. So you are saying that for a real core, in no-load condition there is no leakage flux. The core behaves perfectly. But when it is loaded the leakage flux appears due to the imperfect core?

 

[gorlyu]

Another way to argue would be like this: if the leakage inductance is a result of the imperfect core. Would you not then have different amount of leakage flux for different flux densities in the core (since the permeability varies with flux density)? I.e. you would observe some kind of non-linearity in your leakage inductance.

Or: if the leakage inductance is a result of the imperfect core. Why is the core performance not a factor in the leakage inductance formulas?

All in all, I strongly believe that the answer to question number 2 is yes.gorlyu

 

[jim hardy]

When short-circuiting the secondary you measure a certain leakage inductance.

Question 1: do you agree that the mmfs of each coil are in perfect balance in this case (they cancel - except the magnetization current from the feeding side)?

Question 2: Let's say you replace that core with an ideal core with infinite permeability and no hysteresis or eddy losses. Without changing the coils. Will you still measure that leakage inductance?

Congratulations - your question halfway answered itself. Just needs a little thought now. Apply what you already know..

A picture is often worth a thousand words.
I snipped this from Hyperphysics wonderful transformer page , hopefully they won't mind because snip and paste doesn't cause them extra server traffic.
Annotations in red are mine.

I think you can answer both your questions now.

At zero load current the EDIT primary MMF is only whatever it takes to magnetize the core, secondary MMF is of course zero..

As you allow load current, MMF's go up from there

Remember what inductance is - flux per amp-turn/

old jim

 

[jim hardy]

Would you not then have different amount of leakage flux for different flux densities in the core (since the permeability varies with flux density)? I.e. you would observe some kind of non-linearity in your leakage inductance.

Indeed . You can easily show this with an oscilloscope and a coil of wire.

Hold the coil right next to the laminations of an energized transformer. You will see not a clean sine wave but a distorted one with exaggerated peaks, really rich in third harmonics. . As the flux walks up the B-H curve every cycle that nonlinear reluctance squeezes more flux through the air. It shows up in magnetizing current waveform too...

see http://www.jocet.org/papers/69-A30009.pdf

The blue current wave makes a sine wave flux in iron but not in air. That's why leakage flux looks so peaky.

Try it - sure made the light come on in my brain!(alleged though it is) It's really pronounced on a ferroresonant transformer...

Stay curious, and use everyday experience to figure things out. Every little mystery is an experiment waiting to happen.

old jim

 

[sophiecentaur]

Ok. So you are saying that for a real core, in no-load condition there is no leakage flux. The core behaves perfectly. But when it is loaded the leakage flux appears due to the imperfect core?

In a real core, no load means less current less current means less (nearly zero) voltage loss across the leakage Impedance. That's fair enough, isn't it? If you want to model the leakage as a shunt Leakage Admittance, this admittance would have to be load dependent. So it's not a good equivalent to choose. That's all I'm saying.
None of the components in the equivalent circuit are 'really there' and you have to choose a model with simple equivalent components that actually works. I think that's more or less all there is to it.

 

[jim hardy]

you have to choose a model with simple equivalent components that actually works. I think that's more or less all there is to it.

Amen. It's an approximation that one could refine ad infinitum.
Best IMHO to understand the machine then decide the degree of precision one wants to hold .

old jim

 

[gorlyu]

Hi and thanks for your help Jim and sophiecentaur. I’m starting to tip over for what I firstly didn’t believe in. But this actually means that the leakage flux is not contributing to mmf balance, but the part that is leaking is very very small. Approximately the leakage inductance divided by the magnetizing inductance. Correct?

 

[jim hardy]

I hesitate to agree because i don't know if your words paint the same picture in my mind that you have in yours.

Designers have some control over leakage.

In an everyday power transformer you'd want not much leakage so as to have good regulation. A very few percent is typical.
Big power transformers use it to limit short circuit current.
https://www.fs.fed.us/database/acad/elec/greenbook/10_shortcalc.pdfIn a welder you might want a lot of leakage so that voltage drops rapidly with increasing load, allowing you to strike an arc with substantial voltage but drop to lower voltage to maintain the arc afterward.

Transformers are fun !

 

[sophiecentaur]

Transformers are fun !

Good transformers are HEAVY - is all I can say.

 

[jim hardy]

Good transformers are HEAVY - is all I can say.

I have one that cost me $90 at 30 cents per pound.

 

[gorlyu]

They are fun indeed.

I've been rethinking my transformer knowledge and adjusted it with this new picture and now everything fits.

Thanks!

 

[Tom.G]

I have one that cost me $90 at 30 cents per pound.

And you had these guys unload it for you?

 

[dlgoff]

I have one that cost me $90 at 30 cents per pound.

Photograph?

 

[jim hardy]

I'll snap one and post when Fair Anne's Ipad finishes charging...

 

[Charles Link]

I'm joining this discussion in the middle, but there is one part in the OP's description that I think needs correcting: In general the MMF from the secondary will not balance (and will not be equal and opposite that of the primary). The changing (ac) current in the primary results in a changing flux in the primary, and this same change in flux gets coupled into the secondary, ideally with the ratio of turns. Currents in the secondary can cause a reduction in this changing flux, but if the primary is voltage driven, increased current in the primary will result to keep the changing flux, and thereby both the primary and secondary voltages, at the same level. $\\$ If I understand it correctly, only in the case of a short-circuited secondary will the secondary mmf actually balance the primary mmf. I haven't quite yet figured out how to compute this case though, because mathematically it is unstable in the sense that there are very high currents in both the primary and secondary, unless finite resistances of each are included to maintain some equilibrium. $\\$ And to add to the first paragraph: If it is voltage driven, the mmf of the primary (with unloaded secondary) can be used to compute the resulting ac magnetization of the iron core. This ac magnetization will be virtually independent of the load, and this ac magnetization accounts for causing the change in flux in the core, which in turn generates the EMF (voltage) in the secondary... And a slight correction here: For a given voltage driving the primary, this will allow a computation of the ac magnetic flux in the core, with EMF=voltage=$-\frac{d \Phi}{dt}$, where $\Phi$ is the magnetic flux with the number of turns factor of the primary included. This determines the ac magnetization of the iron core. If you know the magnetic permeability $\mu$ of the iron, you can then compute the mmf, [Edit note: You can compute $H=B/\mu$ from $\Phi= N_p BA$, and then the (unloaded) mmf $=N_p I_{po}=\oint H \cdot \, dl$. As is mentioned in post 27, the net mmf=$N_p I_p-N_s I_s=N_p I_{po}$ will remain constant.] , as well as the primary current with unloaded secondary, assuming no resistive losses in the primary. In the absence of resistance in the primary, the flux $\Phi$ will be independent of any load from the secondary. $\\$ See also https://en.wikipedia.org/wiki/Magnetomotive_force for a discussion of mmf.

 

[jim hardy]

I think you are saying the same thing as this , from post #13

At zero load current ... primary MMF is only whatever it takes to magnetize the core, secondary MMF is of course zero..

As you allow load current, MMF's go up from there

Remember what inductance is - flux per amp-turn/

mmf and current are in exact proportion because mmf is amp-turns..

To use the everyday transformer current equation Ip/Is = Ns/Np we must ignore magnetizing current..
That's equivalent to assuming an infinitely permeable core .
It's not a bad approximation for a quality transformer where magnetizing current is small compared to load current.

To be thorough though one must be aware of magnetizing current so that he can decide whether to include it in whatever problem he is addressing.

 

[Charles Link]

Thank you @jim hardy That pretty much answers my question. From what I wrote above, I was coming to the conclusion, (and I think correctly so), that basically the computation of the mmf's would obey the following: $N_p I_p-N_s I_s=N_p I_{po}$, where $I_{po}$ is the unloaded current in the primary. I have not taken any engineering courses on transformers, but if the primary is voltage driven, this equation would necessarily follow, because $\frac{d \Phi}{dt}$ must stay constant, independent of loading. $\\$ $I_{po}$ is what you refer to above as the magnetizing current, and the approximation is made, as you pointed out, that it is small and basically negligible in many cases. The result is, as you stated, that $N_p I_p=N_s I_s$ which is the statement that the mmf's must balance, as was also stated by the OP. Thank you for clearing that up for me. It was very educational. :) :)

 

[jim hardy]

Thanks Charles
I'm glad you made your post. It is clear you have the concept and if my meandering helps you succinct-ify your explanations that's good !
This thread sure helped me succinct-ify mine.Lavoisier - "Science is but language well arranged" ... I'm always looking for better words , and better thought structure.

old jim

 

[Charles Link]

@gorlyu Depending on how much physics background you have, I think I can add a couple of things that you might find useful:$\\$ There are two Maxwell's equations that are being used in these transformers: The first one is Faraday's law: EMF=voltage $=-\frac{d \Phi}{dt}$. This is the equation that you might expect gets used exclusively, but Ampere's law $\oint B \cdot dl=\mu_o I_{total}$ where $I_{total}=I_{conductors}+I_{magnetic}$ gets utilized in a somewhat unexpected way in the form of $NI=\oint H \cdot dl$. $\\$ To derive this, the equation $B=\mu_o H +M$ is used. This means, (taking curl of both sides), that $\nabla \times B=\mu_o \nabla \times H+\nabla \times M$.The term $\nabla \times M=J_m/\mu_o$ where $J_m$ is the magnetic current density, that most often (for uniform magnetization $M$), shows up as a surface current contribution. When this curl equation is integrated over an area whose outer perimeter is a ring that traverses the the core of the transformer (the loop is inside the core and goes completely around the inside), the result after applying Stokes theorem is a simplified form: $\oint H \cdot dl =NI$. The $M$ part of the $B$, integrated around the loop, in $\oint B \cdot dl=\mu_o I_{total}$ precisely cancels the $\mu_o I_{magnetic}$ portion of $I_{total}$. (i.e. $\oint M \cdot dl=\mu_o I_{magnetic}$). $\\$ The result is the mmf equation $NI =\oint H \cdot dl$, where the number of turns needs to get counted to add up all the current that passes through the plane of the integral. The current here $I$ corresponds to the $I_{conductors}$ term above. $\\$ And in more detail, the complete/net mmf is actually $N_p I_p-N_sI_s$. The secondary term gets a minus sign because the magnetic field that arises from the current in the secondary will always oppose the magnetic field from the current in the primary. $\\$ And I don't want to steer you off the topic, but since you are learning about transformers, you might find this previous post of interest: https://www.physicsforums.com/threads/absolute-value-of-magnetization.915111/

 

[jim hardy]

Photograph?

it was part of an autotransformer based reduced voltage starter .
Was brand new but the guys sort of tossed it around with their big magnet crane...
detail of nameplate

while i was there... how could a fellow pass up an electronic one too?

with these bodacious rectifiers

i think there's enough here to synthesize three phase variable frequency...

sigh. i can't keep up with @dlgoff for creativity though.

old jim