BlackMelon
- 43
- 7
Hi there!
Please refer to the picture below. I would like to understand the equation Curl(H) = J, where H is the magnetic field intensity and J is the current density. So, I inspect a simple problem.
There is a wire carrying current I in the z-axis direction. a_r, a_phi, and a_z are the unit vectors in the directions of the radius, the tangential line, and z-axis, respectively.
So, from H = I/(2*pi*r)a_phi. I take the curl of this vector (in cylindrical coordinate) and got 0. How does this relate to the current density?
Best
BlackMelon
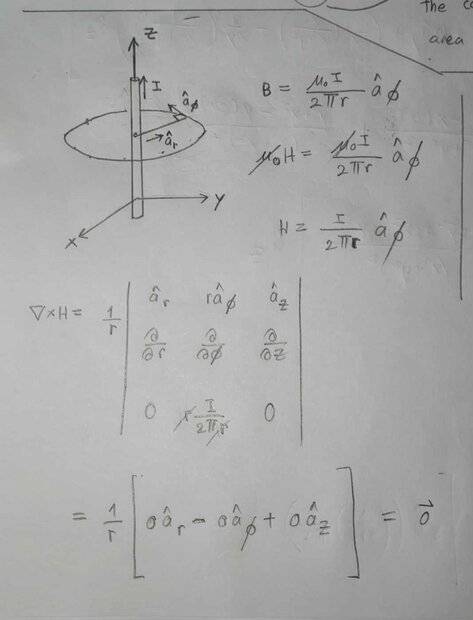
Please refer to the picture below. I would like to understand the equation Curl(H) = J, where H is the magnetic field intensity and J is the current density. So, I inspect a simple problem.
There is a wire carrying current I in the z-axis direction. a_r, a_phi, and a_z are the unit vectors in the directions of the radius, the tangential line, and z-axis, respectively.
So, from H = I/(2*pi*r)a_phi. I take the curl of this vector (in cylindrical coordinate) and got 0. How does this relate to the current density?
Best
BlackMelon