- #1
kidwithshirt
- 11
- 0
Hi all, thanks for reading. This is from my High school AP physics lab and I really couldn't figure out what to do
we attempted to solve this by actually doing the lab instead of using math (which is what you are suppose to do)
I would love to see the mathematical explanation of this. I am in Calculus so anything Calc would not daunt me >.<
http://img181.imageshack.us/img181/7653/physicspd6.th.jpg
An object is tied onto the string the string with the length N. It is dropped at an angle perpendicular to something that holds up the whole system (which is perpendicular to the ground, technically the string should be parallel to the ground) at initial velocity of 0.
But when the object completes 90 degrees of rotation, after it reaches the bottom of the circle, the midsection of the string will hit a rod (that red dot in the middle of the graph) that shortens the length the string by some percent. The distance from top of the system to the rod is M.
The question is, what is the ratio of M/N that will guarantee that the string will complete the rotation (meaning that it goes over 270 degrees from the initial position) AND taut . Well there is a point that it will make the rotation complete, below that the object may rotate more than once.
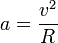
Our lab result is somewhere around 0.6. So if the string is 30cm the rod should be around 18cm.
we attempted to solve this by actually doing the lab instead of using math (which is what you are suppose to do)
I would love to see the mathematical explanation of this. I am in Calculus so anything Calc would not daunt me >.<
Homework Statement
http://img181.imageshack.us/img181/7653/physicspd6.th.jpg
An object is tied onto the string the string with the length N. It is dropped at an angle perpendicular to something that holds up the whole system (which is perpendicular to the ground, technically the string should be parallel to the ground) at initial velocity of 0.
But when the object completes 90 degrees of rotation, after it reaches the bottom of the circle, the midsection of the string will hit a rod (that red dot in the middle of the graph) that shortens the length the string by some percent. The distance from top of the system to the rod is M.
The question is, what is the ratio of M/N that will guarantee that the string will complete the rotation (meaning that it goes over 270 degrees from the initial position) AND taut . Well there is a point that it will make the rotation complete, below that the object may rotate more than once.
Homework Equations
The Attempt at a Solution
Our lab result is somewhere around 0.6. So if the string is 30cm the rod should be around 18cm.
Last edited by a moderator: