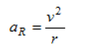bobbsmmith
- 3
- 1
Homework Statement
(a) What is the escape speed from the sun for an object in the Earth's orbit (of orbital radius R) but
far from the Earth? (b) If an object already has a speed equal to the Earth's orbital speed, what
additional speed must it be given to escape as in (a)? (c) Suppose an object is launched from Earth
in the direction of the Earth's orbital motion. What speed must it be given during the launch so
that when it is far from Earth, but still at a distance of about R from the sun, it has that additional
speed calculated in (b) and thus can escape from the sun?
Homework Equations
F = ma
The Attempt at a Solution
I was able to find the answers for parts (a) and (b), but am completely unsure of where to go for part (c). At first, I thought that I needed to find the distance away from the Earth at which the object has a speed of 12.3 km/s (obtained from part (b)), and then use that distance to calculate the velocity of launch. When I did that, I just ended up with the Earth's orbital speed, as calculated in part (b).
1. F = ma = mv^2/R = G * M(sun) * m/R^2
2. v = (G*M(sun)/R)^1/2 = 29.8 km/s
Once I did that, I realized I must not be on the right track. I'm completely unsure of where to begin!