scoomer
- 18
- 4
On page 317 of "INTRODUCTION TO ELECTRODYNAMICS" 4th Ed. by Griffiths he states without proof that the analog to Biot-Savart for finding the E field is:
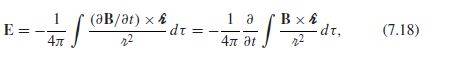
Can anyone direct me to a reference where this is proved or give me a hint how to prove it? Thank you.
Can anyone direct me to a reference where this is proved or give me a hint how to prove it? Thank you.
