Guillem_dlc
- 188
- 17
- Homework Statement
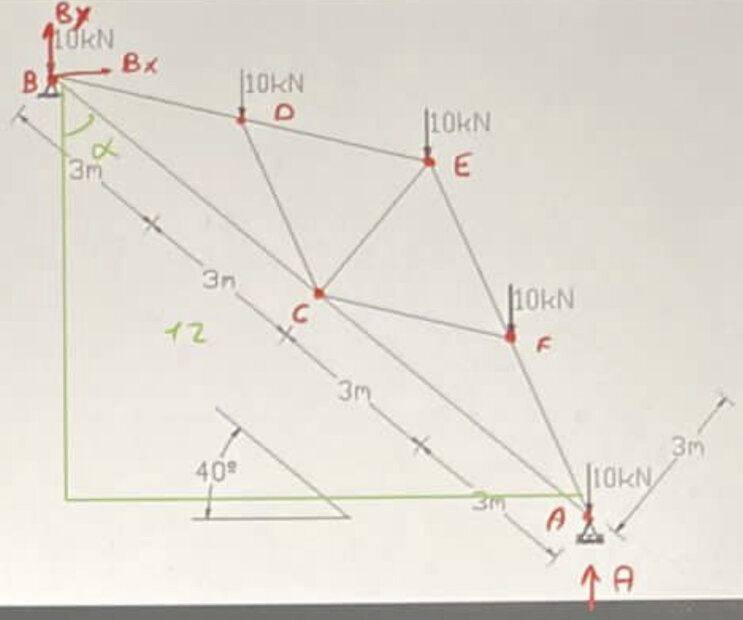
- Solve the following articulated structure.
- Relevant Equations
- ##\sum F=0, \sum M=0##
Figure:
My attempt at a Solution:
We calculate REACTIONS:
$$\sum F_x=0\rightarrow \boxed{Bx=0}\qquad \sum F_y=0\rightarrow By+A=50$$
$$\sum M_B=0\rightarrow \boxed{A=25\, \textrm{kN}}\quad \boxed{B=25\, \textrm{kN}}$$
KNOT B:
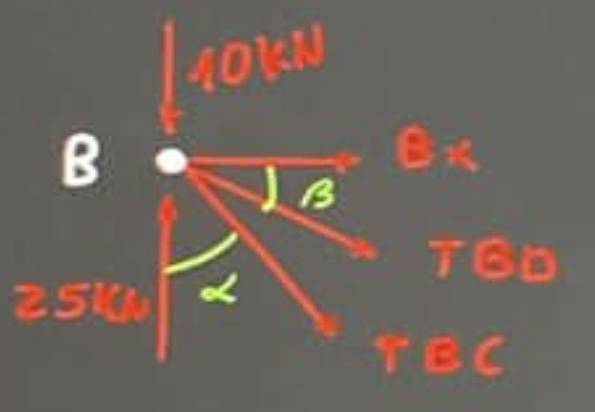
$$\alpha \rightarrow \alpha =90-40=50\, \textrm{º}$$
$$\beta \rightarrow \beta =50+\arctan \left( \dfrac36 \right)-90=13,43\, \textrm{º}$$
$$\sum Fx=0\rightarrow \cancel{Bx}+TBD\cos \beta +TBC\sin \alpha=0$$
$$\sum Fy=0\rightarrow TBD\sin \beta +TBC\cos \alpha=15$$
$$\boxed{TBD=-25,69\, \textrm{kN},\quad TBC=32,62\, \textrm{kN}}$$
Could you look at this one? The solution they give is:
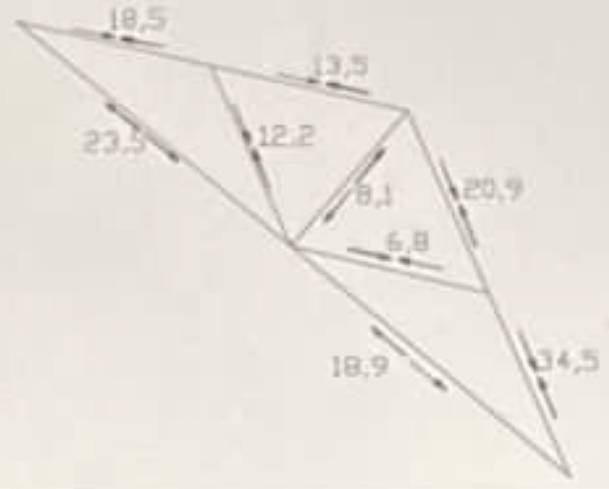
My attempt at a Solution:
We calculate REACTIONS:
$$\sum F_x=0\rightarrow \boxed{Bx=0}\qquad \sum F_y=0\rightarrow By+A=50$$
$$\sum M_B=0\rightarrow \boxed{A=25\, \textrm{kN}}\quad \boxed{B=25\, \textrm{kN}}$$
KNOT B:
$$\alpha \rightarrow \alpha =90-40=50\, \textrm{º}$$
$$\beta \rightarrow \beta =50+\arctan \left( \dfrac36 \right)-90=13,43\, \textrm{º}$$
$$\sum Fx=0\rightarrow \cancel{Bx}+TBD\cos \beta +TBC\sin \alpha=0$$
$$\sum Fy=0\rightarrow TBD\sin \beta +TBC\cos \alpha=15$$
$$\boxed{TBD=-25,69\, \textrm{kN},\quad TBC=32,62\, \textrm{kN}}$$
Could you look at this one? The solution they give is: