greg_rack
Gold Member
- 361
- 79
- Homework Statement
- ARTISTIC BEER CHUGGING CHAMPIONSHIP
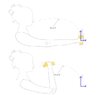
In order to win this championship, a girl has to move a beer from a defined
starting position (when her arm is stretched out) to her mouth, in a stylish manner.
To win, she needs to be majestic(have the center of gravity of the beer to follow a prescribed path, ##f(x,y)=x+30y^2=0##, w.r.t. the coord. system defined as in the figure below), speedy(move the glass to her mouth as quickly as possible) and accurate(always keep her forearm perpendicular to the path):
Initially, as shown in the first figure, she has her arms stretched out with the beer at rest.
Note that in the lower figure, not only her lower arm has moved, but also her
elbow, upper arm and shoulder have translated and rotated.
In this problem, we will limit our scope to the motion of only the lower arm,
which we will model as a simple rod with infinitesimal thickness.
Her lower arm has length of L=0.35 m , with a uniform linear density of
ρ=3.8 kg/m .
The beer (including the glass) has a mass of ##m_{beer}=0.41 kg## .
It is assumed that the beer may be idealised as a point mass.
Due to her limited muscle strength, her upper arm and elbow are only able
to exert the following reaction forces and moments on her lower arm:
-In the axial direction of the lower arm, a force of at most Sn=± 21 N
-In the direction normal to her lower arm, a force of at most St=± 39 N
-Her elbow is able to exert a moment of at most Mcr=± 4.5 N⋅m
At a certain instant in time, the beer is located at y=0.1 m and the velocity
of the beer is equal to ##v_B=5 m/s##. For this instant, compute the following:
-Magnitude of the maximum attainable tangential acceleration she is able to give to the beer
-Magnitude of the corresponding angular acceleration of the arm
-Magnitude of the corresponding reaction force that she should exert on her lower arm
- Relevant Equations
- Relative motion equations
Hello guys, to analyse the above-described situation I have opted for considering the body "beer+lower arm" as a whole, therefore computing the new position of the COM for the correct FBD and equations of motion.
With some uncertainty on the statement of the problem, I have interpreted the values given for maximum ##S_n, S_t, M_{cr}## as(referring to my FBD below) the maximum attainable magnitudes of forces ##F_{En}, F_{Et}, M_E## respectively.

First, would you agree with this?
Assuming this assumption is correct and thus that the forces are those exerted by the elbow joint and muscles on the forearm, I proceeded to writing down the equations of motion for this situation:

From this we can conclude that ##F_{En}## is fixed for a certain(given, for this instant) angular velocity, being just a function of the normal CG acceleration and of the weight(I have assumed, to get to the angular velocity from ##v_B##, that the instantaneous center of zero velocity here is the radius of curvature, given our position along the path).
Using the equations of relative motion, we are able to write down:
$$\mathbf{a_t}=\mathbf{(a_G)_t+ \alpha \times r}\rightarrow \mathbf{(a_G)_t}=\mathbf{a_t-\alpha \times r}$$
(where ##\alpha## is the angular acceleration vector)which, by knowing the directions of the vectors and writing it in scalar form, enables us to substitute for ##(a_G)_t## in the EOM;
We now end up with a system of 5 unknowns(##\alpha, a_t, F_{Et}, F_{En},M_E##) in 3 equations.
Since we are aiming to maximize ##\left \| \mathbf{a_t} \right \|##, what I thought of doing was manipulating the system to write the tangential acceleration in terms of ##F_{Et}## and ##M_E##, to then seek for values of those two forces(into the range given by the problem) so that the value for the tangential acceleration would be maximized, but by doing so, I keep getting to wrong results...
What am I messing up in my analysis?
Last edited: