Angle for maximum height of ball bounce

[Final]

There is a ball of mass m. It is at height L (see the picture).
The kinetic energy is fixed (=E). What is the angle a, for which the ball catches up the maximum height after one bounce?
The bounce is elastic.
Thanks,
Final.

 

[HallsofIvy]

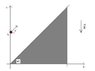
There is a ball of mass m. It is at height L (see the picture).
The kinetic energy is fixed (=E). What is the angle a, for which the ball catches up the maximum height after one bounce?
The bounce is elastic.
Thanks,
Final.

What do you mean by the "maximum height"? If the bounce is perfectly elastic, then at any angle, the ball will bounce back to the maximum height it reached before the first bounce. What that height is will depend on angle. It would be maximum if the ball is moving straight up.

 

[Tide]

Is it a frictionless surface? If not then you have to take the spin acquired by the ball into account.

 

[Final]

Yes, it is a frictionless surface.
The ball cannot go straight up, it must bounce.The height depend by the angle... I won't the angle a(E,L) that maximizes the height AFTER the first bounce. What it succeeds before the bounce not interests me.
Thanks,
Final

 

[Tide]

Method I: Write the trajectory of the ball in the form y = y(x) then find where that trajectory intersects the surface (line) y = x. You can then find the slope of the trajectory. You know the angle of incidence will equal the angle of reflection and you can use that as a starting point to calculate a "new trajectory." Find out how high the ball will travel on the new trajectory. It will be function of \theta and you can attempt to maximize the high point of the trajectory with respect to that angle.

Method II: Try rotating your entire system clockwise by 45 degrees. Be sure to rotate gravity too! You can then follow a procedure similar to Method I but your maximization will be with respect to the direction opposite gravity. I don't know if this will simplify your problem (I haven't tried it!) but my first thought is the geometry might be easier.

 

[Final]

Well,
I have tried both these methods, but my problem is to go on...
Can you solve it?
(I think there is a Method more easy).
Thanks
Final

 

[ehild]

There is a ball of mass m. It is at height L (see the picture).
The kinetic energy is fixed (=E). What is the angle a, for which the ball catches up the maximum height after one bounce?
The bounce is elastic.
Thanks,
Final.

Some hints:

The ball has a given mechanical energy mgh + E. It would rise to the maximum hight if it moved straight upwards vertically after the first bounce.
When the ball bounces back from the slope the magnitude of its velocity stays the same but the direction changes. The direction of its velocity after having reflected from the slope makes the same angle with the normal of the slope as did the incident velocity, only at the other side of the normal. After reflection, the ball moves vertically upward. What was the direction of its velocity before touching the slope?

ehild

 

[Final]

Yes, this is easy: the ball must bounce when it is at the vertex of the parabola... the condition is: 2gL + v^2\sin^2{\Theta} - v^2\sin{2\Theta}=0 (How do you solve this?)
But if the energy is not enough to to catch up the vertex??
Thanks
Final

 

[ehild]

Yes, this is easy: the ball must bounce when it is at the vertex of the parabola... the condition is: 2gL + v^2\sin^2{\Theta} - v^2\sin{2\Theta}=0 (How do you solve this?)
But if the energy is not enough to to catch up the vertex??
Thanks
Final

If the energy is not enough then the problem is just ugly. Apply Tide's method.

OK, I'll think about it.

To solve the equation for \Theta first use that v^2 = 2E/m, rearrange it so as \sin(2\Theta) =2 \sin(\Theta )\cos(\Theta ) is alone at one side, take the square of both sides, replace \cos^2(\Theta) \mbox { by } (1-sin^2(\Theta)), you get a second order equation for \sin^2(\Theta), find the condition that the determinant must not be negative, and solve.


ehild