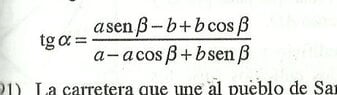Angle of Elevation: Calculating Height of Statue

  • MHB
  • Thread starter leprofece
  • Start date
  • Tags
    Angle
In summary, the conversation discusses a formula that demonstrates the relationship between the angle of elevation, the distance to the column, and the height of a statue on top of the column. It is mentioned that the angle of elevation is represented by x and the distance by a, with a diagram attached for better visualization.
  • #1
leprofece
241
0
(90) on a column stands a statue of length b. From some point
If the foot of the statue with an angle of elevation x. approaching the observation point a distance to the column, the part looks more high from the same angle increased in betha statue. Demonstrate that (see figure)

from figure I see sinalpha/cos(alpha) (a -acosbetha+bsinbetha) = a sen (betha) -b+bcos(betha)
I think this is that I must demonstrateView attachment 2088
 

Attachments

  • Scan.jpg
    Scan.jpg
    10.9 KB · Views: 69
Mathematics news on Phys.org
  • #2
You mention an angle of elevation $x$, but it is not present in the formula attached. What does $a$ represent?

Please attach a diagram so that we can see what the variables actually represent.
 
  • #3
MarkFL said:
You mention an angle of elevation $x$, but it is not present in the formula attached. What does $a$ represent?

Please attach a diagram so that we can see what the variables actually represent.

Sorry
x is alpha in the formula or image
 

FAQ: Angle of Elevation: Calculating Height of Statue

What is the angle of elevation?

The angle of elevation is the angle between the horizontal line and the line of sight from the observer to the top of an object.

How do you calculate the height of a statue using the angle of elevation?

To calculate the height of a statue, you will need to measure the angle of elevation from the ground to the top of the statue. Then, using trigonometric functions such as tangent, you can use the angle and the distance from the observer to the statue to calculate the height.

What other measurements do I need to know in order to calculate the height of a statue using the angle of elevation?

In addition to the angle of elevation, you will also need to know the distance from the observer to the base of the statue. This can be measured using a ruler or measuring tape.

Can the angle of elevation be used to calculate the height of any object?

No, the angle of elevation can only be used to calculate the height of an object that is perpendicular to the ground. For objects that are not perpendicular, other methods such as using shadows or scaling can be used.

Are there any limitations to using the angle of elevation to calculate the height of a statue?

Yes, there are a few limitations. First, the angle of elevation must be measured accurately in order to get an accurate calculation of the height. Additionally, this method assumes that the ground is flat and level, and that the statue is standing straight up. Any discrepancies in these assumptions can affect the accuracy of the calculation.

Similar threads

MHB How Do Shadows and Sun Angles Relate to Tree Height?
Replies
4
Views
937
MHB What is the Height of the Washington Monument from a Distance of 1000 Feet?
Replies
2
Views
976
MHB Find the distance between points C and D if the height of the tree is 4m
Replies
1
Views
2K
MHB Act.ge.5 third angle of triangle
Replies
1
Views
982
MHB Calculating Elevation Angle to Hit Target at 100 m and 10 m
Replies
5
Views
2K
MHB Find the Angle of Parable Tangent from Human Running Step
Replies
1
Views
2K
MHB What Is the Height of the Pole in This Trigonometry Problem?
Replies
6
Views
2K
MHB How Is Trigonometry Used to Calculate Flagpole Heights?
Replies
4
Views
3K
MHB Calculating Height and Distance of a Mountain at Sea
Replies
8
Views
2K
MHB Angle of elevation and depression problems
Replies
1
Views
3K

Hot Threads

Recent Insights

Back
Top