AshNotKetchum
- 8
- 0
Homework Statement
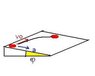
A physics student playing with an air hockey table (a frictionless surface) finds that if she gives the puck a velocity of 3.44 m/s along the length (2.73 m) of the table at one end, by the time it has reached the other end the puck has drifted 2.08 cm to the right but still has a velocity component along the length of 3.44 m/s. She correctly concludes that the table is not level and correctly calculates its inclination from the above information. What is the angle of inclination?
Relevant equations
Summing forces in x and y directions, according to the question.
The attempt at a solution
I could not visualize a way to solve this question using Newton's laws. The only path to a solution I could visualize was to assume that 2.08 cm was the hypotenuse of a triangle in which the height was the distance the puck had 'fallen', and then solve for theta. However, finding out the distance the puck had fallen has proved to be insurmountable and I may very well be trying to solve this question incorrectly.
A physics student playing with an air hockey table (a frictionless surface) finds that if she gives the puck a velocity of 3.44 m/s along the length (2.73 m) of the table at one end, by the time it has reached the other end the puck has drifted 2.08 cm to the right but still has a velocity component along the length of 3.44 m/s. She correctly concludes that the table is not level and correctly calculates its inclination from the above information. What is the angle of inclination?
Relevant equations
Summing forces in x and y directions, according to the question.
The attempt at a solution
I could not visualize a way to solve this question using Newton's laws. The only path to a solution I could visualize was to assume that 2.08 cm was the hypotenuse of a triangle in which the height was the distance the puck had 'fallen', and then solve for theta. However, finding out the distance the puck had fallen has proved to be insurmountable and I may very well be trying to solve this question incorrectly.