Intoto
- 5
- 1
Hey all, so I’ve been learning nonlinear acoustics and have encountered a conceptual hurdle in my studies. When using a model, such as a form of the classical Burgers equation, to propagate sound waves, you generally have a “characteristic angular frequency” in the equation (often represented by omega). For a simple sine wave, this is very easy to understand. However, let’s say the wave to be propagated is a discrete, non-sinusoidal pulse.
I have attached an illustration below as an example of what I am talking about.
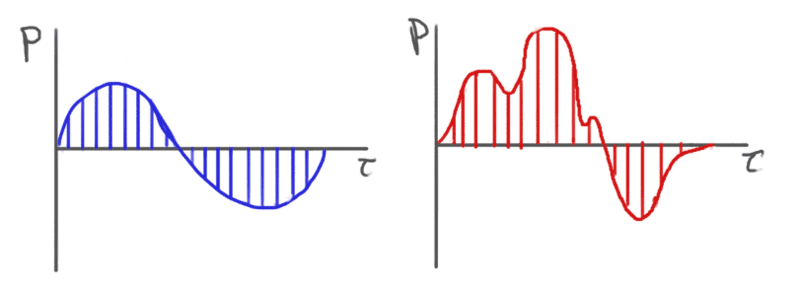
(Excuse my art skills, blue is supposed to be a uniformly sampled sin wave and red is supposed to be a uniformly sampled pulse.)
I am unsure of what the “characteristic angular frequency” is supposed to represent when using a wave such as the single, non-sinusoidal pulse. I am assuming that it may require the use of Fourier transforms (which I am vaguely familiar with), but I am unsure of what I would even be looking for (e.g. a fundamental frequency, or perhaps a different frequency at every point in the waveform).
Any insight would be greatly appreciated.
I have attached an illustration below as an example of what I am talking about.
(Excuse my art skills, blue is supposed to be a uniformly sampled sin wave and red is supposed to be a uniformly sampled pulse.)
I am unsure of what the “characteristic angular frequency” is supposed to represent when using a wave such as the single, non-sinusoidal pulse. I am assuming that it may require the use of Fourier transforms (which I am vaguely familiar with), but I am unsure of what I would even be looking for (e.g. a fundamental frequency, or perhaps a different frequency at every point in the waveform).
Any insight would be greatly appreciated.