Angular frequency of plank attached to spring

[vetgirl1990]

Homework Statement

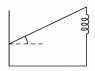
A horizontal plank (mass 2kg, length 1m) is pivoted at one end. A spring (k=1000N/m) is attached at the other end. Find the angular frequency for small oscillations.

Answer: ω=39rad/s

Homework Equations

ω = √(mgd + kΔxd/I)
I think I would be treating the plank as a long thin rod with rotational axis through the end (since I'm not provided with the dimensions of the plank), so I = 1/3mL² + md²
Where L: length of the rod, d: distance between pivot and rod's centre of mass (d=L/2)

The Attempt at a Solution

I = 1/3mL² + md² = 1/3mL² + m(L/2)²

ω = √(mgd + kΔxd/I)
mgd component --> mg(L/2)
kΔxd component --> mg(L/2)²

Substituting all the known values...
ω = √[(2)(9.8)(1/2) + 1000(1²)] / [(1/3)(2)(1²) + 2(1/2)²]
ω = √1009.8/1.16 = 29.4

Still not getting the correct answer.

 

[haruspex]

$I = 1/3mL^2 + md^2 = 1/3mL^2 + m(L/2)^2$

Not so.