- #1
FG_313
- 17
- 1
This (photo) is a very typical example of conservation of angular momentum, but my trouble arrises from trying to prove that the difference of energy will have to correspond to work, by calculating the work done by you to alter the moment of inertia. I have spent a lot of time in this, but I still can't understand it satisfactorily. I'll try to explain my reasoning (for the few parts that I managed to do) and post my points of confusion as they arrise, and if there is anything you want to correct or add, it would be certainly very helpfull.
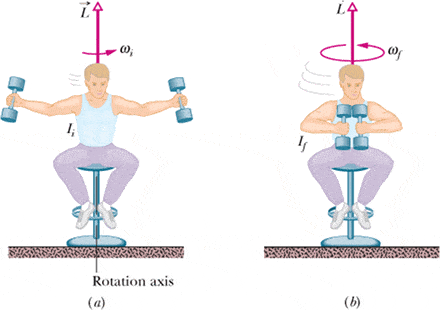
No external torques => L is constant => Iω is constant. Therefore, the angular velocity goes up when we close our arms.
Now, looking at the rotational KE, it`s clear that is not conserved. That is not itself a problem: you do work in this situation. I woud like to look at it in a more quantitativaly way. Let`s approximate the situation in the first place for this:
Two masses M, each with a distance r to the axis (the situation is always symmetrical!). In this case, it can be checked (done it!) that the difference in KE when the masses are at r1 and after at r2 is equal to the work done by "fighting" the centrifugal force on the both ways (by the way, I'm not certain why we don't need to take into account the coriollis force, it is normal to the displacement in the radial direction, so the first thing I thought is that the work has to be zero. However, if I were to apply the "formula" W=∫τdφ when τ is the torque done by fighting the corriollis force, it would lead to apparent contradiction). But this is oversimplificating too much the situation, I'm not satisfied. The following treatment is where I'm having more problems:
Your torso, head, legs and all that will be treated as a cilinder, or any other rigid body with moment of inertia Io, the weights are connected to you by a massless rod and the weights are pontual masses with mass M (each one of them). Let r be the distance between the axis and one of the weights, the total moment of inertia would then be: I=Io+2Mr^2. I want to calculate the work done by bringing the masses from distance r1 to r2, taking the assumptions described, and I'm having trouble with that. Here are some other thoughts on the matter:
If we take into account only the rigid body (Io), he goes from Io*ω1 to Io*ω2, so there has to be a external torque to this system (only the rigid body- No weights!). That would probably be done by the force done by the weights (M), that are a reaction (Newton 3rd law) to the force I have to make to beat the corriolis force. So I guess this torque has to be taken in account when calculating the work done! Than, We cannot ignore the corriolis force when calculating work, like we did in the first case. Furthermore, the thing that makes the first case so easy so easy to work with, is that the centrifugal force has a simple relation to the angular mommentum, which is constant, so the integral of work gives the correct answer. Thank you for the attention!
No external torques => L is constant => Iω is constant. Therefore, the angular velocity goes up when we close our arms.
Now, looking at the rotational KE, it`s clear that is not conserved. That is not itself a problem: you do work in this situation. I woud like to look at it in a more quantitativaly way. Let`s approximate the situation in the first place for this:
Two masses M, each with a distance r to the axis (the situation is always symmetrical!). In this case, it can be checked (done it!) that the difference in KE when the masses are at r1 and after at r2 is equal to the work done by "fighting" the centrifugal force on the both ways (by the way, I'm not certain why we don't need to take into account the coriollis force, it is normal to the displacement in the radial direction, so the first thing I thought is that the work has to be zero. However, if I were to apply the "formula" W=∫τdφ when τ is the torque done by fighting the corriollis force, it would lead to apparent contradiction). But this is oversimplificating too much the situation, I'm not satisfied. The following treatment is where I'm having more problems:
Your torso, head, legs and all that will be treated as a cilinder, or any other rigid body with moment of inertia Io, the weights are connected to you by a massless rod and the weights are pontual masses with mass M (each one of them). Let r be the distance between the axis and one of the weights, the total moment of inertia would then be: I=Io+2Mr^2. I want to calculate the work done by bringing the masses from distance r1 to r2, taking the assumptions described, and I'm having trouble with that. Here are some other thoughts on the matter:
If we take into account only the rigid body (Io), he goes from Io*ω1 to Io*ω2, so there has to be a external torque to this system (only the rigid body- No weights!). That would probably be done by the force done by the weights (M), that are a reaction (Newton 3rd law) to the force I have to make to beat the corriolis force. So I guess this torque has to be taken in account when calculating the work done! Than, We cannot ignore the corriolis force when calculating work, like we did in the first case. Furthermore, the thing that makes the first case so easy so easy to work with, is that the centrifugal force has a simple relation to the angular mommentum, which is constant, so the integral of work gives the correct answer. Thank you for the attention!