I How Does the Book's Formula for Angular Momentum Differ from Mine?

[Kashmir]

A disc initially has angular velocities as shown

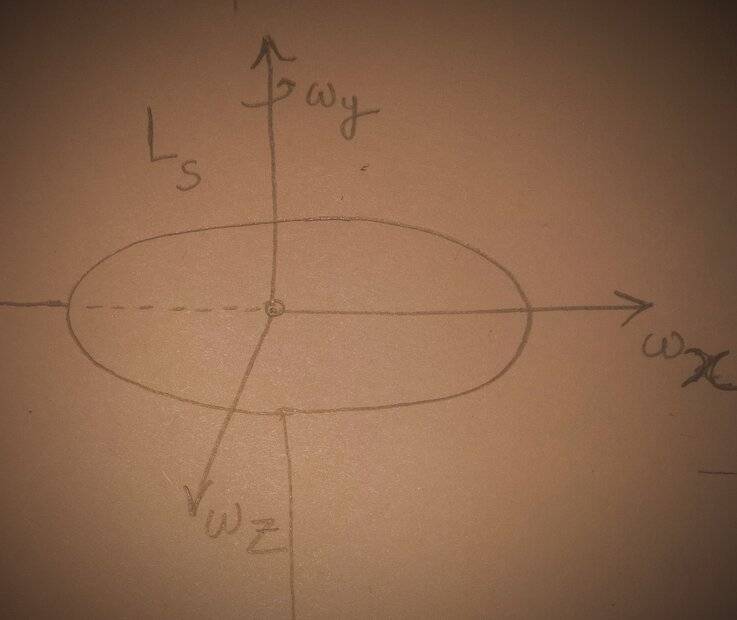
It's angular momentum along the y-axis initially is $L_s$
I tried to find its angular momentum and ended up with this:$L=I_{x} \omega_{x}+I_{y} w_{y}+I_{z} z_{z}$The z component of angular momentum is thus $L_{z}=I_{z} \omega_{z}$

However I found a similar situation in a book

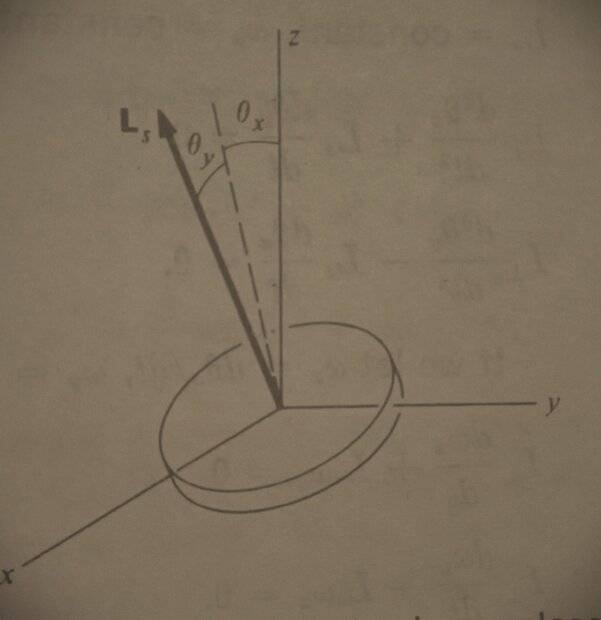
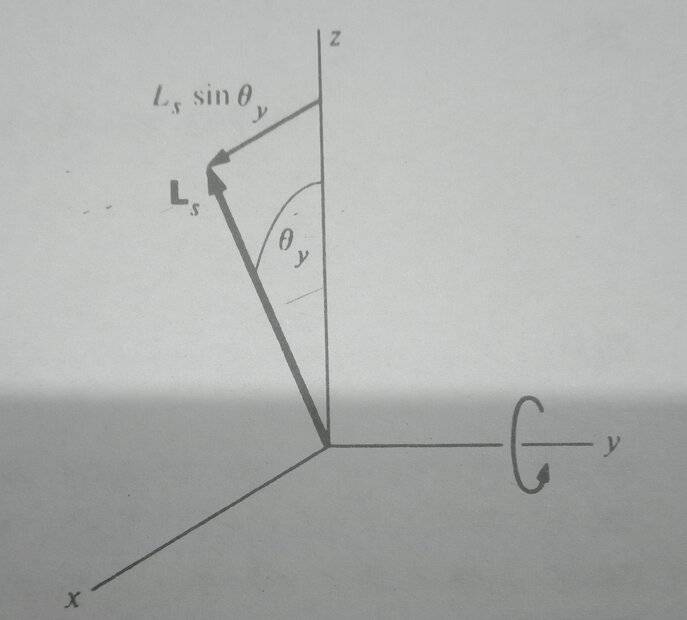
that writes the components of angular momentum along x as $L_{x}=I_{x x} \frac{d \theta_{x}}{d t}+L_{s} \sin \theta_{y}$

The book has an additional term $L_{s} \sin \theta_{y}$ for the angular momentum which I don't.

Why am I wrong ?

 

[Charles Link]

Your question is not completely clear. Perhaps the disc is initially spinning with an $L_s$ and then given an additional rotation. Otherwise a magnetization of the disc could also make for an $L_s$, but in general $L_s$ from any magnetization would be very small.

 

[RPinPA]

Are you asking for an expression for the angular momentum of a disk where the rotation axis is not perpendicular to the disk? Your drawing is not clear.

Are $\omega_x, \omega_y$ and $\omega_z$ the cartesian coordinates of $\vec\omega$? How are $I_x$, $I_y$ and $I_z$ defined? Can you describe your calculations?