- #1
spursfan2110
- 21
- 0
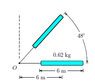
A uniform rod of mass 0.62 kg is 6 m long.
The rod is pivoted about a horizontal, fric-
tionless pin at the end of a thin extension (of
negligible mass) a distance 6 m from the cen-
ter of mass of the rod. Initially the rod makes
an angle of 48◦ with the horizontal. The rod
is released from rest at an angle of 48◦ with
the horizontal, as shown in the figure.
What is the angular speed of the rod at
the instant the rod is in a horizontal position?
The acceleration of gravity is 9.8m/s2 and the
moment of inertia of the rod about its center
of mass is I = (1/12)mL2
Answer in units of rad/s.
U = mgh
KE = .5Iw2
So, I set U = KE
mgh = .5Iw2
Then I plugged in the moment of inertia
mgh = .5(1/12)(mass of rod)(length of rod)2w2
Cancelled out the m and solved for the height of the center of mass
g(6sin(48degrees)) = .5(1/12)mL2w2
and finally, I plugged in values and solved.
(9.8)(6sin(48 degrees)) = .5(1/12)(6)2w2
And solved for w, which I found to equal 5.397339822.
This is wrong, but I have no idea where my error is. Can you guys help me spot it??
The rod is pivoted about a horizontal, fric-
tionless pin at the end of a thin extension (of
negligible mass) a distance 6 m from the cen-
ter of mass of the rod. Initially the rod makes
an angle of 48◦ with the horizontal. The rod
is released from rest at an angle of 48◦ with
the horizontal, as shown in the figure.
What is the angular speed of the rod at
the instant the rod is in a horizontal position?
The acceleration of gravity is 9.8m/s2 and the
moment of inertia of the rod about its center
of mass is I = (1/12)mL2
Answer in units of rad/s.
Homework Equations
U = mgh
KE = .5Iw2
The Attempt at a Solution
So, I set U = KE
mgh = .5Iw2
Then I plugged in the moment of inertia
mgh = .5(1/12)(mass of rod)(length of rod)2w2
Cancelled out the m and solved for the height of the center of mass
g(6sin(48degrees)) = .5(1/12)mL2w2
and finally, I plugged in values and solved.
(9.8)(6sin(48 degrees)) = .5(1/12)(6)2w2
And solved for w, which I found to equal 5.397339822.
This is wrong, but I have no idea where my error is. Can you guys help me spot it??