Angular velocity of a falling rod?

[spursfan2110]

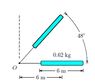
A uniform rod of mass 0.62 kg is 6 m long.
The rod is pivoted about a horizontal, fric-
tionless pin at the end of a thin extension (of
negligible mass) a distance 6 m from the cen-
ter of mass of the rod. Initially the rod makes
an angle of 48◦ with the horizontal. The rod
is released from rest at an angle of 48◦ with
the horizontal, as shown in the figure.
What is the angular speed of the rod at
the instant the rod is in a horizontal position?
The acceleration of gravity is 9.8m/s2 and the
moment of inertia of the rod about its center
of mass is I = (1/12)mL²
Answer in units of rad/s.

Homework Equations

U = mgh
KE = .5Iw²

The Attempt at a Solution

So, I set U = KE

mgh = .5Iw²

Then I plugged in the moment of inertia

mgh = .5(1/12)(mass of rod)(length of rod)²w²

Cancelled out the m and solved for the height of the center of mass

g(6sin(48degrees)) = .5(1/12)mL²w²

and finally, I plugged in values and solved.

(9.8)(6sin(48 degrees)) = .5(1/12)(6)²w²

And solved for w, which I found to equal 5.397339822.

This is wrong, but I have no idea where my error is. Can you guys help me spot it??

 

[thrill3rnit3]

parallel axis theorem, since the system is not rotating about its center of mass

 

[Redsummers]

Yeah, you have to use Steiner's theorem to work out the inertia at that point.

 

[spursfan2110]

So if I read my stuff right, instead of inserting (1/12)mL² for momentum, I would insert (1/12)mL² + md²?