AdkinsJr
- 148
- 0
This is a problem right out of the text of my calculus book. So I actually have the work, but I'm confused about something the did.
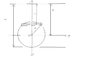
Problem: Find the hydrostatic force on one end of a cylindrical drum with radius 3 ft. if the drum is submerged in water 10 ft deep.
I attached a diagram
Pressure can be defined:
p=density, d=distance below the surface
P=pgd=\delta d
The area of the ith strip is:
A_i=2\sqrt{9-(y^*_i)^2}\Delta y
The average distance below the surface is:
d_i=7-y^*_i
Then when they write the pressure, they give:
\delta_i=62.5(7-y^*_i)
The implies that pg=62.5.
The density of water is p=62.4 lb/ft^3
http://en.wikipedia.org/wiki/Density_of_water
Gravitational acceleration is 32.174 ft/s^2
So how does \delta d_i=pgd_i=62.5(7-y^*_i) ? Is this an error? It seems that they accidently neglected to account for gravitational acceleration.
Problem: Find the hydrostatic force on one end of a cylindrical drum with radius 3 ft. if the drum is submerged in water 10 ft deep.
I attached a diagram
Pressure can be defined:
p=density, d=distance below the surface
P=pgd=\delta d
The area of the ith strip is:
A_i=2\sqrt{9-(y^*_i)^2}\Delta y
The average distance below the surface is:
d_i=7-y^*_i
Then when they write the pressure, they give:
\delta_i=62.5(7-y^*_i)
The implies that pg=62.5.
The density of water is p=62.4 lb/ft^3
http://en.wikipedia.org/wiki/Density_of_water
Gravitational acceleration is 32.174 ft/s^2
So how does \delta d_i=pgd_i=62.5(7-y^*_i) ? Is this an error? It seems that they accidently neglected to account for gravitational acceleration.