Application of Ampère-Maxwell equ.

[quasar987]

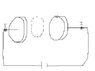
Consider the set-up illustrated in the attachement. The radius of the capacitor plates is a. The field btw the plates varies according to

\vec{E}(t) = \frac{It}{\epsilon_0 \pi a^2}\hat{z}

(z is to the right)

So since the current enclosed is 0, Ampere-Maxwell law in its integral form after evaluation of the integral of d\Phi_E/dt reads...

\oint \vec{B}\cdot d\vec{l} = \mu_0 I \frac{s^2}{a^2}

s being the radius of my amperian loop.

What is the argument according to which B is solenoid and constant along the path of integration? In the case of magnetostatic, it was the right-hand thumb rule (i.e. the Biot-Savart law) that allowed us to determine the orientation of B. But now what is it that permits to conclude?

 

[quasar987]

Looks like I forgot to add the picture doesn't it.

 

[cliowa]

I'm not really sure I understand what you want to know (what do you mean exactly when saying "What is the argument according to which B is solenoid and constant along the path of integration?"), but I'll just suppose you want to know why you can assume the magnitude of the B-field to be the same around your loop. The answer is: a symmetry argument (cylindrical symmetry).
But then I don't get what you're talking about "right-hand thumb rule" and "Biot-Savart". This has nothing to do with assuming the magnitude of the B-field to be constant along your loop.

Hoping to get some clearer input next time...Cliowa

 

[quasar987]

But then I don't get what you're talking about "right-hand thumb rule" and "Biot-Savart". This has nothing to do with assuming the magnitude of the B-field to be constant along your loop.
Hoping to get some clearer input next time...Cliowa

In the case of say a straight current wire in which a current I circulates, what allows you to conclude that the field is in the chape of concentric circles around the wire and constant in magnitude on the contour of each circles? It is the Biot-Savart law, which tells you B is in the direction of

\vec{I} \times \frac{\vec{r}-\vec{r}'}{|\vec{r}-\vec{r}'|}

(using Griffith'Ssnotation). This is the "right-hand thumb rule": let your thumb point in the direction of I; then your fingers curl in the direction of B.

In order to say that

\oint \vec{B}\cdot d\vec{l} =B2\pi s

one must show that

i) B is constant in magnitude on the contour of the amperian circle.

ii) B is tangent to the amperian circle (so the dot product has no \cos\theta term)

The "right-hand thumb rule" is used to verify the property ii).

Also in the case of the straight current wire, B is constant in magnitude on the contour by a simple symetry argument: Consider a point anywhere is space. Now rotate the wire along its axis or make the point travel along a circular path centered on the wire: nothing changes AT ALL. Hence the field has no choice but to be the same everywhere along the circular path.

I'm not really sure I understand what you want to know (what do you mean exactly when saying "What is the argument according to which B is solenoid and constant along the path of integration?"), but I'll just suppose you want to know why you can assume the magnitude of the B-field to be the same around your loop. The answer is: a symmetry argument (cylindrical symmetry).

I have strong reasons to believe that in the case of the magnetic field of my problem, B also satisfies the conditions i) and ii). But I don't have an equation for \vec{B} in terms of dE/dt (i.e. the equivalent of Biot-Savart). So how do I know what the B field created by a chnaging electric field looks like?

I can see why it is constant along the amperian circle though.