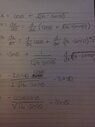Colin2
- 9
- 0
I need help solving all three parts to this question, never seen a question regarding applications of differentiation that is this hard before!
View attachment 4094
All help is much appreciated.
View attachment 4094
All help is much appreciated.