themadhatter1
- 139
- 0
Homework Statement
Homework Equations
The Attempt at a Solution
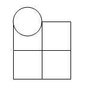
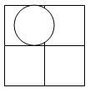
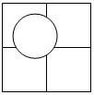
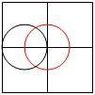
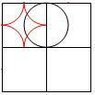
I found this interesting problem in my textbook. I have heard of Buffon's needle experiment which estimates pi through probability. This problem came from a pre-calc book out of the probability section. The problem seams similar to Buffon's needle in that d is the diameter of the coin as well as the distance in between each square. However, this is a coin and a grid, not parallel lines and a needle. I'm not sure whether the question is asking for an analytical solution to b or an actual experiment. Can it be determined analytically?
The probability for hitting a vertex would be the same for any d value chosen. I believe it would be much more likely to hit a vertex than to land exactly in between two parallel lines. Does finding the probability involve the area taken up if a coin were placed in each square grid, and the free space left?