Are my graphs and answers correct for position, velocity, and acceleration?

  • Thread starter Miike012
  • Start date
  • Tags
    Graphs
In summary, the conversation is about a person's post of a picture that translates information into graphs. They are asking for confirmation on the correctness of their answers and graphs. The graphs show the position, velocity, and acceleration of a ball as it moves left and right. The person also asks for help plotting the graphs on one graph.
  • #1
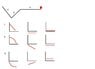
Miike012
1,009
0
I posted a picture that translates the bottom information into a graph
I wanted to know if my answers below are correct and my graphs are correct...
Thank you.
First Graph:Position
second Graph : Velocity
third graph: Accelertaion

Position Velocity Acceleration

1. Ball rolls to the left of A + - 0
2. Ball rolls to the left down B + - -
3. Ball rolls to the left up C - - +
4. Ball reaches its maximum - 0 ?
height at c
5.Ball rolls to the right up C - + +
6. Ball rolls to the right up B + + -
7. Ball rolls to the right across A + + -
 

Attachments

  • phy.JPG
    phy.JPG
    11.6 KB · Views: 441
  • phy 2.JPG
    phy 2.JPG
    10.8 KB · Views: 440
Physics news on Phys.org

FAQ: Are my graphs and answers correct for position, velocity, and acceleration?

How do I know if my graphs are accurate?

One way to ensure accuracy is to double-check your data and calculations. You can also use statistical tests or consult with a colleague to review your graphs.

What should I do if my graphs don't match my hypothesis?

If your graphs do not support your hypothesis, it is important to re-evaluate your data and methodology. You may need to adjust your hypothesis or conduct further research to determine the reason for the discrepancy.

How can I make my graphs easier to read and understand?

To make your graphs more visually appealing and easier to understand, you can use clear and concise labels, appropriate colors and scales, and avoid clutter and unnecessary information.

Is there a specific format or style to follow when creating graphs?

There are several commonly used formats, such as bar graphs, line graphs, and pie charts. It is important to choose the most appropriate format for your data and research question, and to follow any guidelines provided by your institution or journal.

What should I do if I notice errors in my graphs after they have been published?

If you notice errors in your published graphs, you should contact the publisher or journal to request a correction. It is important to be transparent and honest about any mistakes in your research.

Similar threads

Distance-time graph of a ball throw vertically up from a fixed point
Replies
5
Views
1K
Constant velocity, constant acceleration?
Replies
11
Views
2K
A ball climbing a ramp while "rolling the wrong way"
Replies
32
Views
2K
Horizontal impulse on a ball at rest on a plane (with friction)
Replies
14
Views
2K
Experimentally calculating the acceleration due to gravity
Replies
13
Views
2K
Finding acceleration from Velocity vs Position graph
Replies
2
Views
3K
A child rolls a marble....Plot graphs etc.
Replies
4
Views
5K
Which Force is Represented by the Gradient of the Ball-Wall Collision Graph?
Replies
3
Views
3K
Two balls, dropped with a delay of ##\Delta t##, meet after rebound
Replies
34
Views
1K
Potential energy of ball thrown upwards
Replies
5
Views
13K

Hot Threads

Recent Insights

Back
Top