Are the sum of all forces written correctly for this system?

AI Thread Summary
The discussion focuses on verifying the setup of the Sum of All Forces for a given system. A participant points out that the component of weight in the x direction is missing from the calculations. The correct equation for Σ FxB is provided, incorporating the necessary forces. Additionally, it is noted that since the velocity is constant, the net acceleration (ma) equals zero. The mention of the 30-degree angle raises questions about its relevance in the context.
Blockade
Messages
68
Reaction score
0
Member advised to use the formatting template for questions posted to the homework forums
Can someone check if my Sum of All Forces is setup correctly?

Problem:
7b189141b5.jpg


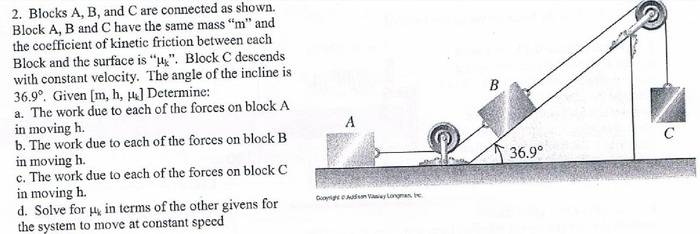
Diagram:
http://puu.sh/o6pLY/285d7b12c1.jpg

Sum of all Forces:
2e23f577b3.jpg
 
Last edited by a moderator:
Physics news on Phys.org
Blockade said:
Can someone check if my Sum of All Forces is setup correctly?

Problem:
[ IMG]http://puu.sh/o6pGI/7b189141b5.jpg[/PLAIN]

Diagram:
[ IMG]http://puu.sh/o6pLY/285d7b12c1.jpg [/PLAIN]

Sum of all Forces:
2e23f577b3.jpg
You're missing a force in Σ FxB, namely the component of weight in the x direction.
 
Last edited by a moderator:
SammyS said:
You're missing a force in Σ FxB, namely the component of weight in the x direction.

Σ FxB: -mgsin(30 degrees) + T2 - T1 - μkmgcos(30 degrees) = ma

Thank you.

and all ma = 0 since velocity is constant
 
By the way: Why 30° ?
 
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Pulley system problem: 6 Pulleys and 1 Mass
Replies
5
Views
856
Block and pulley on movable incline
Replies
2
Views
2K
Ideal Vs Real Mass Pulley system
Replies
10
Views
5K
Dynamics of Circular Motion
Replies
12
Views
451
Calculating acceleration of a prism and block connected to a wall through a rope and pulley
Replies
4
Views
318
Electric Potential Energy of Point Charge Systems
Replies
2
Views
875
Pulley system -- Calculate the mass that balances this pulley system
Replies
2
Views
1K
Simple closed force system -- Mechanics
Replies
9
Views
2K
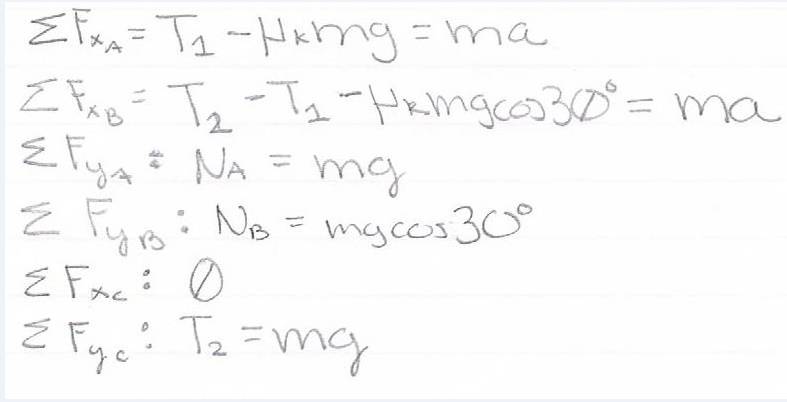
Olympiad dynamics problem with 3 masses and a pulley
Replies
17
Views
2K
Block on top of an inclined plane, with a rough surface, that moves with constant acceleration
Replies
41
Views
3K

Hot Threads

Recent Insights

Back
Top