- #1
pkc111
- 225
- 26
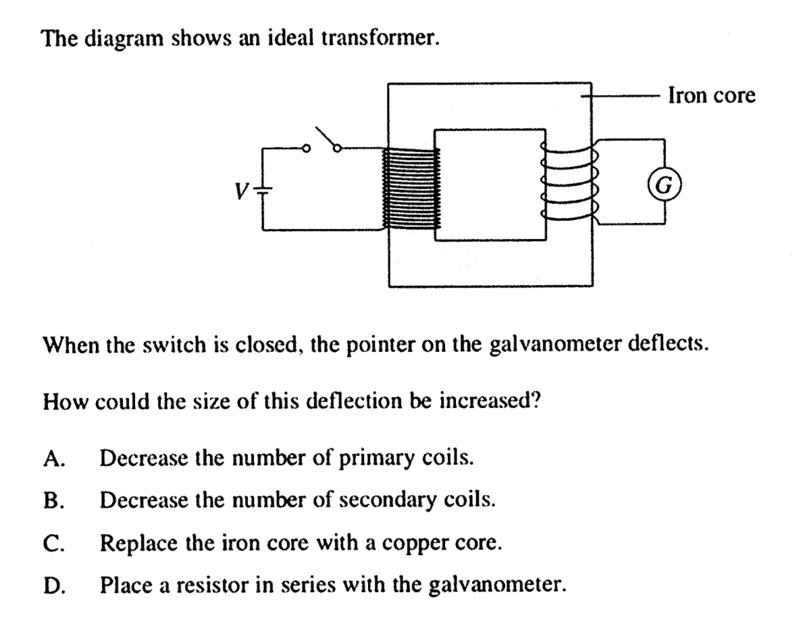
- Homework Statement
- See below
- Relevant Equations
- n1/n2 = V1/V2
V1I1 = V2I2
Answer B would increase the n1/n2 ratio and increase the deflection. Making it correct.
But also, Answer A would increase the current through the primary coil, and hence the power. This would increase the power in the secondary coil hence I2, leading to lower voltage V2. Making it also correct.
My other question, do Galvanometers like described in this question, function as voltmeters or ammeters?
But also, Answer A would increase the current through the primary coil, and hence the power. This would increase the power in the secondary coil hence I2, leading to lower voltage V2. Making it also correct.
My other question, do Galvanometers like described in this question, function as voltmeters or ammeters?
Last edited: