Area Under a Curve, 3D, with known end points and curve radius

[geetar_king]

I am trying to find out a method of determining the area below a curve.

The end points of the curve are known in cartesian space, and the curvature of the curve is known.

A diagram of the curve is here, shown in the images belowthis webpage

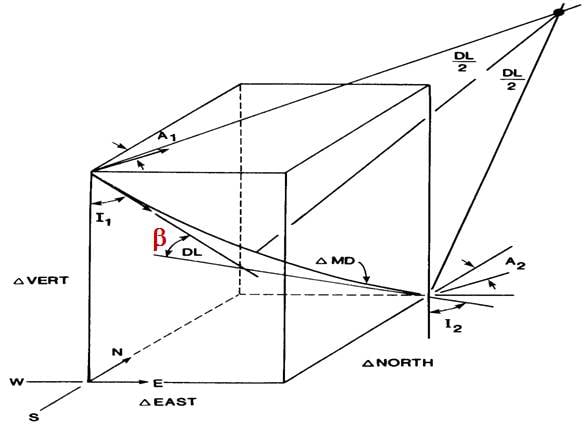
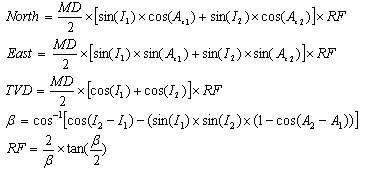
ß must be in radians

Where;
MD = Measured Depth between surveys in ft
I1 = Inclination (angle) of upper survey in degrees
I2 = Inclination (angle) of lower in degrees
Az1= Azimuth direction of upper survey
Az2 = Azimuth direction of lower survey
RF = Ratio Factor
ß is the dog leg angle.

I'm trying to find the area between the curve and a line projected downwards onto the bottom plane.

I have a wellbore trajectory which gives x,y,z, coordinates (northing,easting,vertical depth)and the angle DL, and I am trying to find the net area above and below a certain depth plane by using the wells directional survey.

Any suggestions would be appreciated, thanks!

 

[fresh_42]

The plane along which you project is given by a linear equation. It can be written in a form $z=\ldots$ or another variable. This substituted into the equation of the curve gives a new equation of the curve with only two coordinates. Easiest would be to write the curve as $y=f(x)$ and integrate it.