Jdtbtb_sp
- 4
- 0
May I know how to calculate this question without a calculator? The final answer of this question is 3 but I really have no idea how to work on it to get the final answer.
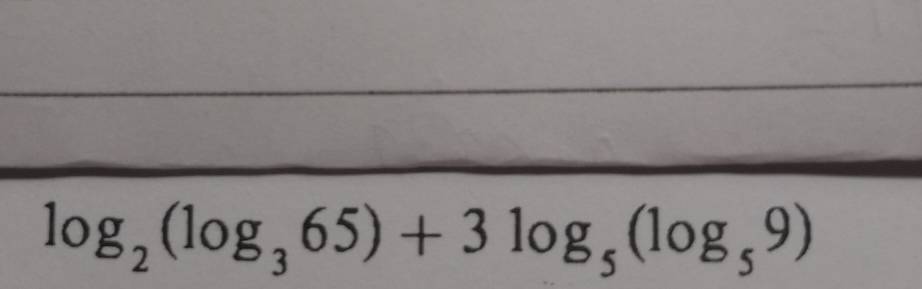
Last edited: