Sabertooth
- 29
- 2
- Homework Statement
- Astronomical Calculus:Spaceship Dilation problem
- Relevant Equations
- t'=t(√-1(v^2/c^2)). Integral Calculus.
Hi everyone. I have provided myself a problem that I insist on solving, however, I want to do it "the right way" where I can put every parameter into a calculator and get an answer quickly. I pondered doing it manually and figured that it could be done to a reasonable precision in an hour or two, but that is not enough for me to consider this problem solved. I want to use formal calculus to put the parameters into an equation and get the answer.
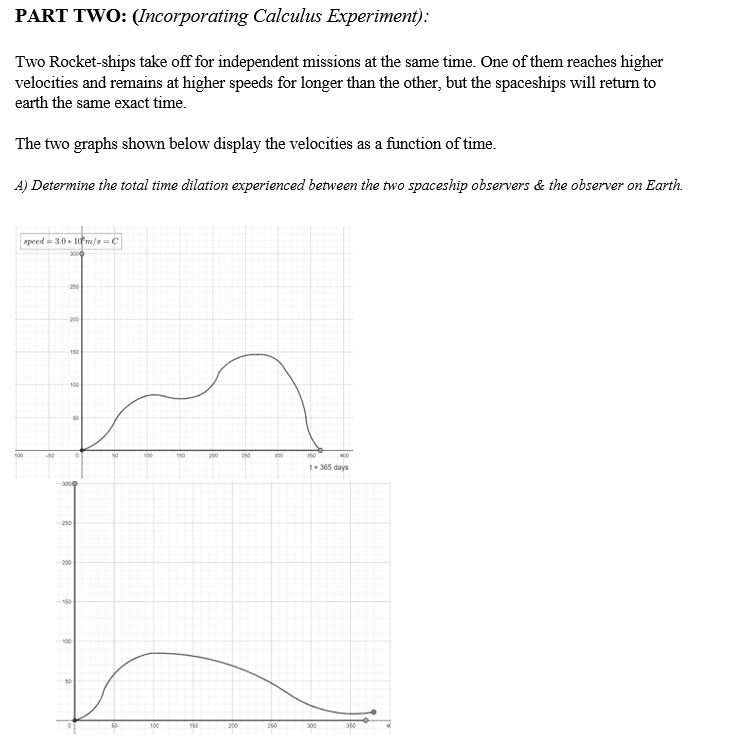
Is there any calculus aficionados that could help me get all the ingredients for solving this problem here, and getting a result. This problem relates purely to Special Relativity & Velocity⋅. General Relativity can be ignored for all intents and purposes.
Is there any calculus aficionados that could help me get all the ingredients for solving this problem here, and getting a result. This problem relates purely to Special Relativity & Velocity⋅. General Relativity can be ignored for all intents and purposes.