mooncrater
- 215
- 18
Consider the algorithms :
This algorithm finds the successor of an element in a Binary Search Tree. Here, x is the pointer to the node whose successor we have to find, and TREE-MINIMUM(x) finds the minimum in a tree whose root is x. The running time of this algorithm is ##O(h)##, where h is the height of the tree.
Now the question is:
Prove that no matter what node we start at in a height-h binary search tree, k successive calls to TREE-SUCCESSOR take ##O(k+h)## time.(where h is the height of the tree.)
(clrs 12.2-8)
I've assumed that "successive calls" mean that we find the successor of the element, which came out to be the successor in the last use of TREE-SUCCESSOR.
Now, we know that in a BInary Search Tree, the left most element is the least element. Thus, starting from the leftmost element.
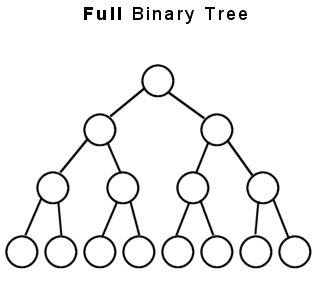
In this image, we've a tree of height 3. When we start from the left-most node, we get the following number of loop runs for successive elements:
##1,1,2,2,1,1,3,3,1,1,2,2,1,1##
thus we can group sub-parts of this sequence :
## (1,1,2,2,1,1),3,3,(1,1,2,2,1,1)##
For maximum number of total loop runs for k successive calls, we start from the ##3,3##, i.e. the ##h,h##, where h is the height of the tree.For example,
If ##k=2##
then we take the ##3,3##
If ##k=4## then we include the ##1,1## from either of the sides.
Similarly, if ##k=8## we take one of the ##2,2## from either of the sides.
Now, we assume that ##(1,1,2,2,1,1)## are whole blocks, and that the sequence is symmetric, so it's basically the two times of:
##3,1,1,2,2,1,1##
Thus generally, two times of:
##h,1,1,2,2,1,1,h-1,h-1,1,1,2,2,1,1,h-2,h-2,...##
Since, I halved the sequence, values of ##k## are also halved.
Thus an approximate value of this summation would be:
$$ 2 \times \frac {(k/2 -1)} {6} \times 8 + 2 \times (\frac { k/2} {8})( h + \frac { k/2} {8} -1 ) $$
Number of such blocks are : ## 2 \times (\frac { k/2 -1} {6}) \times 8##
as we go through the halved sequence, we used ##k/2 ## and multiplied by 2. Since there are 6 elements in each block and their sum is 8, therefore division by the former and multiplication by the former is done.
We tackle the ##h,h-1,h-1,h-2,h-2## by finding the number of such terms, i.e ## \frac { k/2 }{8}## and the summation of such terms is done using the summation of an Arithmetic progression.(Though only ##h## is used, instead of ##2\times h##.)
This summation yields an upper bound of ##O(k\times h)## instead of ##O(k+h)##.
So, where am I wrong? Any help appreciated.
Code:
TREE-SUCCESSOR(x)
1. if x.right_child !=NIL
2. return TREE-MINIMUM(x.right_child)
3. y=x.parent
4. while y != NIL and x == y.right_child
5. x = y
6. y = y.parent
7. return y
Code:
TREE-MINIMUM(x)
1. while x.left_child != NIL
2. x = x.left_child
3.return xThis algorithm finds the successor of an element in a Binary Search Tree. Here, x is the pointer to the node whose successor we have to find, and TREE-MINIMUM(x) finds the minimum in a tree whose root is x. The running time of this algorithm is ##O(h)##, where h is the height of the tree.
Now the question is:
Prove that no matter what node we start at in a height-h binary search tree, k successive calls to TREE-SUCCESSOR take ##O(k+h)## time.(where h is the height of the tree.)
(clrs 12.2-8)
I've assumed that "successive calls" mean that we find the successor of the element, which came out to be the successor in the last use of TREE-SUCCESSOR.
Now, we know that in a BInary Search Tree, the left most element is the least element. Thus, starting from the leftmost element.
In this image, we've a tree of height 3. When we start from the left-most node, we get the following number of loop runs for successive elements:
##1,1,2,2,1,1,3,3,1,1,2,2,1,1##
thus we can group sub-parts of this sequence :
## (1,1,2,2,1,1),3,3,(1,1,2,2,1,1)##
For maximum number of total loop runs for k successive calls, we start from the ##3,3##, i.e. the ##h,h##, where h is the height of the tree.For example,
If ##k=2##
then we take the ##3,3##
If ##k=4## then we include the ##1,1## from either of the sides.
Similarly, if ##k=8## we take one of the ##2,2## from either of the sides.
Now, we assume that ##(1,1,2,2,1,1)## are whole blocks, and that the sequence is symmetric, so it's basically the two times of:
##3,1,1,2,2,1,1##
Thus generally, two times of:
##h,1,1,2,2,1,1,h-1,h-1,1,1,2,2,1,1,h-2,h-2,...##
Since, I halved the sequence, values of ##k## are also halved.
Thus an approximate value of this summation would be:
$$ 2 \times \frac {(k/2 -1)} {6} \times 8 + 2 \times (\frac { k/2} {8})( h + \frac { k/2} {8} -1 ) $$
Number of such blocks are : ## 2 \times (\frac { k/2 -1} {6}) \times 8##
as we go through the halved sequence, we used ##k/2 ## and multiplied by 2. Since there are 6 elements in each block and their sum is 8, therefore division by the former and multiplication by the former is done.
We tackle the ##h,h-1,h-1,h-2,h-2## by finding the number of such terms, i.e ## \frac { k/2 }{8}## and the summation of such terms is done using the summation of an Arithmetic progression.(Though only ##h## is used, instead of ##2\times h##.)
This summation yields an upper bound of ##O(k\times h)## instead of ##O(k+h)##.
So, where am I wrong? Any help appreciated.