- #1
iScience
- 466
- 5
http://i.imgur.com/QFRCRZr.jpg (the black numbers are just so i can make references throuhout this thread, they're not part of my notes)
(z is the partition function for Boltzmann statistics)
so the first four lines is just expanding an expression for the average internal energy of a system in terms of the partition function z.
the argument of line 7 is that since line 6 is in the same form as line 4, it must be equal to the avg internal energy.
----------------
Okay so, i understand lines 1~4. the problem is on line 5, but first i want to discuss the partition function.
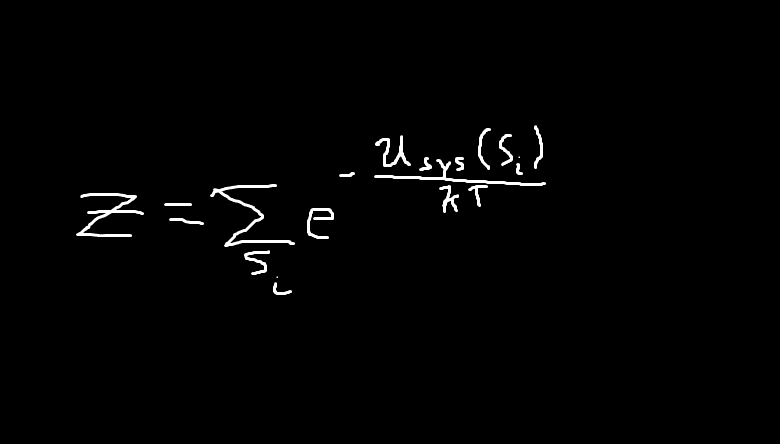
So the energies for all the available states to a system are summed up. in other words the numerator of the power is -Uall. So when we take the derivative of this function w/ respect to the quantity 'kT' in line 5, if we are to leave this just in terms of the -Usys(Si), instead of simply writing.. Uall, then ALL the terms must be enclosed by the sum. So then if this is the case, then in line 6, the..
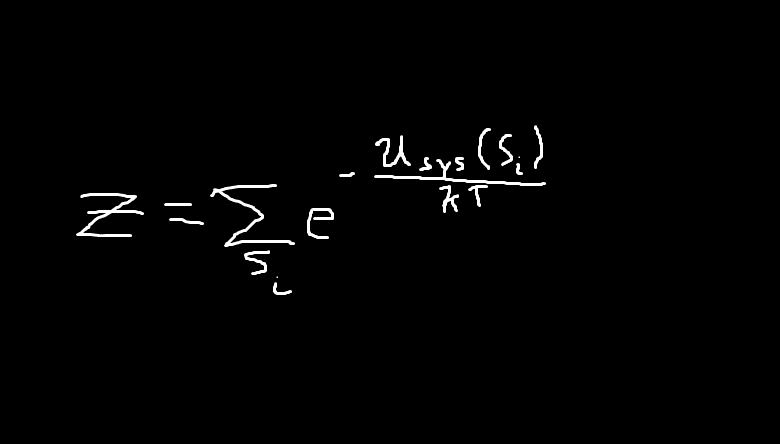 ..term should also be enclosed by the sum. If this is the case, then that is just z, and this should cancel with the 1/z term.
..term should also be enclosed by the sum. If this is the case, then that is just z, and this should cancel with the 1/z term.
This is wrong, but i just don't know where i went wrong. please do ask me to clarify something if you are confused
thanks
(z is the partition function for Boltzmann statistics)
so the first four lines is just expanding an expression for the average internal energy of a system in terms of the partition function z.
the argument of line 7 is that since line 6 is in the same form as line 4, it must be equal to the avg internal energy.
----------------
Okay so, i understand lines 1~4. the problem is on line 5, but first i want to discuss the partition function.
So the energies for all the available states to a system are summed up. in other words the numerator of the power is -Uall. So when we take the derivative of this function w/ respect to the quantity 'kT' in line 5, if we are to leave this just in terms of the -Usys(Si), instead of simply writing.. Uall, then ALL the terms must be enclosed by the sum. So then if this is the case, then in line 6, the..
This is wrong, but i just don't know where i went wrong. please do ask me to clarify something if you are confused
thanks
Last edited: