Undergrad Average of the B-field over a volume and surface integrals

[Aaron121]

Purcell says that taking the surface integral of the magnetic field $\textbf{B}$ over the surfaces $S_{1}, S_{2}, S_{3},...$ below is a good way of finding the average of the volume integral of $\textbf{B}$ in the neighborhood of these surfaces.

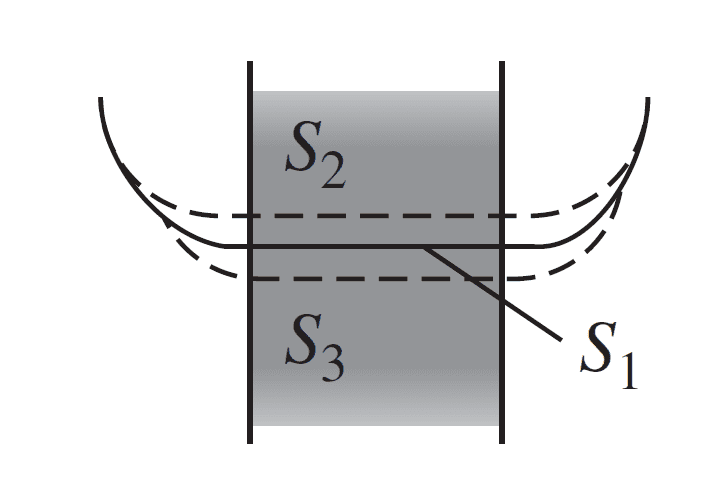
More specifically, he says in page $553$ of the third edition,

Now taking the surface integral over a series of equally spaced planes like that is a perfectly good way to compute the volume average of the field $\textbf{B}$ in that neighborhood, for it samples all volume elements impartially.

I can't really see the connection between the volume average of $\textbf{B}$ over, say, the volume between $S_2$ and $S_3$ $$\frac{1}{V}\int \textbf{B} dv$$ and the surface integrals of $\textbf{B}$ over $S_2$ and $S_3$ $$\int_{S_3} \textbf{B}\cdot d\textbf{s}_{3},~~\int_{S_2} \textbf{B} \cdot d\textbf{s}_{2}.$$ Any indications?

 

[Delta2]

This looks like it is some application of divergence theorem but I can't figure it out.

Also the way the surfaces are given in the figure, if we apply gauss's law in integral form for the magnetic field and in the closed surface consisting of $S_2$+ $S_3$ we can conclude that it is $$\oint_{S_2+S_3} \mathbf{B}\cdot d\mathbf{s}=0 \Rightarrow \iint_{S_2} \mathbf{B}\cdot d\mathbf{s_2}=-\iint_{S_3}\mathbf{B}\cdot d\mathbf{s_3}$$

 

[Delta2]

One other thing I can think of, and especially that the figure provided inspires me to think, is by using some interpolation technique to be able to compute $$f(x)=\iint_{S_x}\mathbf{B}\cdot d\mathbf{s_x}$$ for any parallel plane surface $S_x$ between $S_2$ and $S_3$, and then to compute the volume integral
$$\iiint |\mathbf{B}|dV\approx\int_{x_2}^{x_3} f(x)dx$$