momentum
- 111
- 0
<Moderator's note: Please upload images for otherwise the links might get broken.>
Here is the backward difference table given in my book
https://prnt.sc/n2965l
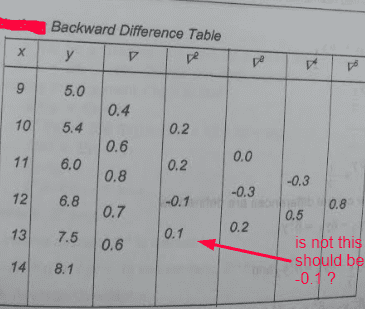
But it seems this table is wrong. I have marked my comment in the screen.
Can you please tell who is right ?
Here is the backward difference table given in my book
https://prnt.sc/n2965l
But it seems this table is wrong. I have marked my comment in the screen.
Can you please tell who is right ?