- #1
BillKet
- 312
- 29
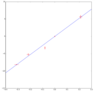
Hello I have these points coming from different experiments:
##x = [-0.3, -0.2, -0.09, 0.01, 0.2]##
##y = [-8.15, -5.20, -3.32, 0., 5.65]##
##y_{err} = [0.1, 0.27, 0.35, 0.09, 0.44]##
and I need to fit a straight line to them (based on theoretical arguments). I attached below the obtained fit. I get for the slope ##26.30\pm1.03## . It is quite clear that the for the 3rd points something went wrong in the experiment and they didn't account for some systematics (it is actually the first measured point), as there is no motivation for that point to be that far (about 3 sigma) from the fit. But this is the data and I can't really change it. However, I assume that my value of the slope is biased by that point (especially because the error it has is not that big) and probably it leads to a bigger error on the estimate of the slope. Do you have any advice on what I should do? Should I just use these values? Should I just remove that point by hand? Should I add some lower weight to it in the fit? Thank you!
##x = [-0.3, -0.2, -0.09, 0.01, 0.2]##
##y = [-8.15, -5.20, -3.32, 0., 5.65]##
##y_{err} = [0.1, 0.27, 0.35, 0.09, 0.44]##
and I need to fit a straight line to them (based on theoretical arguments). I attached below the obtained fit. I get for the slope ##26.30\pm1.03## . It is quite clear that the for the 3rd points something went wrong in the experiment and they didn't account for some systematics (it is actually the first measured point), as there is no motivation for that point to be that far (about 3 sigma) from the fit. But this is the data and I can't really change it. However, I assume that my value of the slope is biased by that point (especially because the error it has is not that big) and probably it leads to a bigger error on the estimate of the slope. Do you have any advice on what I should do? Should I just use these values? Should I just remove that point by hand? Should I add some lower weight to it in the fit? Thank you!