milky9311
- 5
- 0
Q: "If a curve with a radius of 85m is properly banked for a car traveling 65km/h, what must be the coefficient of static friction for a car not to skid when traveling at 95km/h?"
[PLAIN]http://a4.sphotos.ak.fbcdn.net/hphotos-ak-ash4/215513_1974874979462_1470693940_32310002_1293630_n.jpg
2. The attempt at a solution
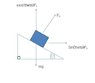
I found theta
FNcos(theta) = mg
(mgsin(theta))/cos(theta) = (mv2)/r
theta = 21.4o
But next bit i couldn't do.
Wouldnt the centripetal force of the 95km/h car be FNsin(theta) + musFN? as the static friction + the horizontal component of the normal force allows circular motion?
thanks
[PLAIN]http://a4.sphotos.ak.fbcdn.net/hphotos-ak-ash4/215513_1974874979462_1470693940_32310002_1293630_n.jpg
2. The attempt at a solution
I found theta
FNcos(theta) = mg
(mgsin(theta))/cos(theta) = (mv2)/r
theta = 21.4o
But next bit i couldn't do.
Wouldnt the centripetal force of the 95km/h car be FNsin(theta) + musFN? as the static friction + the horizontal component of the normal force allows circular motion?
thanks
Attachments
Last edited by a moderator: