Addie
- 9
- 0
Banked Curves involving friction
Problem: A car is traveling in a circle of a radius of 50 meters, on the surface the coefcient of static friction between the car's tires and the road is .3. With a banking angle of 30 degrees.
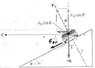
(I attached a diagram)
So here's what's known:
Radius: R=50 m
Coeffcient of Static Friciton: us=.3
Bank angle theta: T=30 deg
First find: Maximum velocity.
I found this by knowing...
Sum of Fx: m(v^2/r)=NsinT+UsNcosT
Sum of Fy: NcosT-UsNsinT-mg
I find by Equation = Square root of{[rg (sinT+UsCost)]/CosT-(.3 x sinT)}
IT results in Vmax= 22.8 m/s
(here is where I found that equation)
PART 2
Find the apparent weight (hint apparent wieght = Fn)
This the part I'm struggling with.
So i use my Sum of Fx to find N ;
m(v^2/r)=NsinT+UsNcosT=
m(v^2/r)=(mgcosT)sinT+Us(mgcosT)cosT
m(v^2/r)=m[(gcosT)sinT+Us(gcosT)cosT]
then I get nowhere because I divide through by M, and I need to find M or N itself and its practically impossible with just this information...
please help if you can.. any help is apreciated..
Problem: A car is traveling in a circle of a radius of 50 meters, on the surface the coefcient of static friction between the car's tires and the road is .3. With a banking angle of 30 degrees.
(I attached a diagram)
So here's what's known:
Radius: R=50 m
Coeffcient of Static Friciton: us=.3
Bank angle theta: T=30 deg
First find: Maximum velocity.
I found this by knowing...
Sum of Fx: m(v^2/r)=NsinT+UsNcosT
Sum of Fy: NcosT-UsNsinT-mg
I find by Equation = Square root of{[rg (sinT+UsCost)]/CosT-(.3 x sinT)}
IT results in Vmax= 22.8 m/s
(here is where I found that equation)
PART 2
Find the apparent weight (hint apparent wieght = Fn)
This the part I'm struggling with.
So i use my Sum of Fx to find N ;
m(v^2/r)=NsinT+UsNcosT=
m(v^2/r)=(mgcosT)sinT+Us(mgcosT)cosT
m(v^2/r)=m[(gcosT)sinT+Us(gcosT)cosT]
then I get nowhere because I divide through by M, and I need to find M or N itself and its practically impossible with just this information...
please help if you can.. any help is apreciated..
Attachments
Last edited: