Discussion Overview
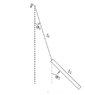
The discussion revolves around calculating the kinetic energy of a bar suspended by a rope at one of its ends, specifically focusing on the contributions from translational and rotational motion. Participants explore different approaches to determine the kinetic energy, considering the bar as a pendulum and discussing the implications of its motion.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant questions whether to calculate kinetic energy based on the center of mass or the bar-rope junction, suggesting the former may be correct.
- Another participant notes that the kinetic energy consists of translational kinetic energy at the center of mass and rotational kinetic energy, emphasizing that these values may change due to the motion of the bar.
- There is a discussion about which moment of inertia to use for calculations, with options being I = (m L^2)/12 for rotation about the center of mass or I = (m L^2)/3 for rotation at the beginning of the bar.
- A participant expresses confusion regarding the differences in kinetic energy calculations when comparing scenarios with and without the rope, particularly regarding the motion of the center of mass and rotational motion.
- Clarification is provided that the total kinetic energy includes both translational energy and rotational energy around the center of mass.
- One participant reflects on their own calculations and realizes the correctness of their approach after initially expressing confusion.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the best approach to calculate kinetic energy, as there are differing opinions on which moment of inertia to use and how to account for the motion of the center of mass. The discussion remains unresolved regarding the implications of different scenarios on kinetic energy calculations.
Contextual Notes
Participants mention various assumptions about the system, such as whether the rope is ideal and the specific motion of the bar, which may affect the calculations and interpretations of kinetic energy.