- #1
wvcaudill2
- 54
- 0
Homework Statement
lim as x[itex]\rightarrow[/itex]-1 = [itex]\frac{|x^{2}-1|}{x^{2}+x}[/itex]
Homework Equations
N/a
The Attempt at a Solution
Tried to write this as a piecewise function, but I got lost.
wvcaudill2 said:Ok, from the left-hand side of the limit, I got -2, and from the right-hand side I got 2,
and when x-1=0 I got "does not exist."
wvcaudill2 said:I do not see how they should be switched. Can you explain your process in more detail?
wvcaudill2 said:Im still not sure how it is you are coming to the statement that "if x comes from the left, then this expression is positive." Can you explain how you are getting this?
Here is what I have now:
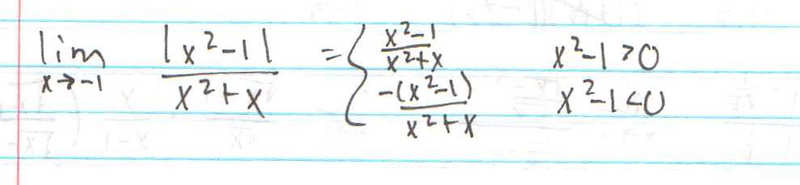
wvcaudill2 said:Ok, I see what you are saying now, but when I graphed the parabola, I also saw that coming from the right-hand side, the values of x were also positive up until x=1.
A basic limit involving absolute value is a mathematical concept that involves determining the value that a function approaches as the input approaches a specific value, while also taking into account the distance from that value, or the absolute value.
To calculate a limit involving absolute value, you can use the definition of a limit, which states that the limit of a function at a specific value is equal to the value that the function approaches as the input approaches that value. This can be represented algebraically using the absolute value function.
The absolute value is important in limit calculations because it allows us to consider both positive and negative values as the input approaches a specific value, rather than just the distance from that value. This is necessary for certain functions, such as piecewise functions, where the behavior may differ on either side of the specific value.
Yes, there are a few special cases for limits involving absolute value. One example is the case where the absolute value is inside of a trigonometric function. In this case, the limit may not exist if the function oscillates rapidly as the input approaches the specific value.
Limits involving absolute value can be applied in many real-world situations, such as calculating the maximum and minimum values for a given function, or determining the rate of change of a function at a specific point. They can also be used in economics and physics to model various scenarios and predict outcomes.