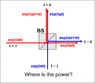
Beam Splitter: were is the power?

[Alexander-1]

http://physics.nad.ru/img/bs1.gif
Let us consider beamsplitter BS.
2 rays are incident on it as shown in figure.
During reflection the waves are shifted by phase at pi.
As a result I=0 in both directions.
Where is the power lost?

 

[lalbatros]

To answer the question, I would use an energy "balance box" around the beam splitter.
This would give a simple and obvious answer.
You could even make the "balance box" smaller and confine it to the narrow region where reflexion and transmission occurs.

The next question would be: what happens actually, when you switch on the light source?
Another question: how would you build such a BS? And then describe again what happens.
Yet another question: descibe what would happen in a more realistic way.
(like taking into account some un-ideal properties of the materials used)

 

[lpfr]

To answer the question, I would use an energy "balance box" around the beam splitter.
This would give a simple and obvious answer.
You could even make the "balance box" smaller and confine it to the narrow region where reflexion and transmission occurs.

The next question would be: what happens actually, when you switch on the light source?
Another question: how would you build such a BS? And then describe again what happens.
Yet another question: descibe what would happen in a more realistic way.
(like taking into account some un-ideal properties of the materials used)

I'm sorry to say that I do not found much sense in your post. It would be marvelous that you enlighten us with the "simple and obvious answer". I'm not a youngster, but I do not see the "obvious answer".
No need to build such BS. You can buy it. It is a standard object.

 

[Sojourner01]

The 'empirical' answer I'd give - based on what you know to be true from the thought experiment - is that all the power in the beams is going into the beam splitter. This is the case because there is actually no beam at all passing from either face - they're extinct due to complete destructive interference.

Therefore, I'd say the two light beams are merely heating up the beam splitter; or in a real world situation, scattering from it. I'm afraid I'm not able to propose a mechanism of how this could occur.

 

[Alexander-1]

Another question: how would you build such a BS?

http://www.redoptronics.com/cube-beamsplitter.html"
or we can use semireflected mirror http://physics.nad.ru/img/bs2.gif

It seems I1 + I2 = const
http://physics.nad.ru/img/bs3.gif
How to prove?

 

[lalbatros]

lpfr,

By "simple and obvious answer" I mean that I would spoil your pleasure if I told you the answer.
I would also infringe the homework policy of this forum.

Well ...

Let's imagine you built the BS from a suitable thin layer of refractive material.
This thin layer will be a resonator and will accumulate energy.
That's simple as that, and that's what a simple balance tells us immediately.

Don't you believe energy balance is easy and useful?

If this material has a small absorption coefficient, this will limit the field in the layer when a stationary state is reached.
Remember about the "quality factor" of a resonator and its role in the response to the applied fields.
Without any absorption, no stationary state would be possible.

Now, more fun is possible:

If the absorption coefficient of the thin layer is very small, a long transient could be observed after switch-on of the light source.
Do you think the intensities I1 and I2 will also be zero?
If no, could you describe the evolution in some more detail?

Note:
====
I used BS in the past in a laser-scattering experiment.
I also used similar devices for milimeter waves scattering experiments.
My question was pedagogical.
I dislike useless abstraction, I like that people see concretely what they are talking about.

 

[lpfr]

Thanks Lalbatross.
I do not think that this was a homework..
I do not think that the answer is "simple and obvious".
I understand that you consider the layer between the two prisms as a resonator.
When you put only one beam, the losses in the resonator are negligible, if I believe the specs of commercial BS. This means that the amplitude is limited.
When you put the other beam, the situation is the same.
But, when you put the two beams, the amplitude in the resonator grows (in order to have big losses) and the amplitude at the exit drops to zero.
I do not see the physical process. I cannot visualize the amplitude that I must have in one side of an interface layer-prism to have zero amplitude in the other side. The only possibility that I see, is zero amplitude in the two sides.
This means also that, if you use a very low losses material for the layer, the amplitude in the resonator will grow very high.
Is this used to obtain non-linear effects?
If you make a theoretical BS with no losses, will this mean that the amplitude will grow indefinitely? (Theoretically, of course).
Can you give me some explications?
Thanks again.

 

[Alexander-1]

This thin layer will be a resonator and will accumulate energy.

There is no resonator there. Any other ideas?

 

[lalbatros]

Alexander-1,

There is a resonator there.
The "blocking" thin layer that makes up the BS works exactly as a resonator in the situation you proposed.
Go to the theory of thin layers and think about it.
Further, the energy balance is very clear about the conclusion: energy accumulates in the BS ... unless it is absrobed.

lpfr,
You are right in your description.
If the losses are negligible, the field within the BS will grow indefinitively.
The purpose of a BS is of course not to increase the field until disruption.


Generally speaking,
it is interresting or funny to consider this problem in a non-stationary state.
Just as for laser, the field within the cavity is not stationary, so here the field -after switch on- is not stationary within the thin layer of the BS.
Even more: if the absorption was really neglible, the BS would never be able to work exactly as described, because the interfences would not match perfectly with a rising internal field in the thin layer.

I think it should not be too complicated to write down the non-stationary equations for this system. We could consider an exponential switch-on to make things even simpler: in that case the usual Laplace-transform methods are totally similar to the Fourier-transform methods and the "usual" approach to this kind of problems. No calculations! Just adding an imaginary part to the frequency !

 

[lalbatros]

Well friends,

Maybe I was plain wrong ...
Coudn't it be that the beams are reflected back to the source?
How can we decide if that happens really?
Any idea?

 

[Alexander-1]

Well friends,
Maybe I was plain wrong ...
Coudn't it be that the beams are reflected back to the source?
How can we decide if that happens really?
Any idea?

A couple years ago I saw in this forum an explanation of this effect. For this reason I write to here again. From my experience with optical fibers it seems that I1+I2=const, but I can not prove it. -- http://physics.nad.ru/img/bs3.gif -- That is, when intensity in arm 1 is maximal, the intensity in arm 2 is minimal and vice versa. In fiber optic couplers there is effect of consumption of energy, but it seems this is not our case. Maybe phase shift is not equal to pi in this case. I shall think and hope to listen your ideas on this.

 

[lalbatros]

Another possibility is that the energy is lost along along the direction of the thin film. (along the diagonal of your drawing)

 

[lpfr]

Yes. I draw the direction of rays transmitted and reflected in the layer and I found the same situation than in a waveguide. In fact the power is not being lost in the layer. The power is being transmitted in the layer in the direction right and up in the drawing. Light must exit in the upper right edge of the cube.

 

[Cthugha]

or we can use semireflected mirror

Semireflected (is this the right word?) mirrors won't work here as the phase difference between transmitted and reflected wave in such beam splitters is not pi, but pi/2. Modeling them as mirrors concerning the reflected part while doing nothing to the transmitted wave is not an appropriate description, which makes complete destructive interference impossible.

I am not sure about other beam splitter designs, though.

At least Mandel and Wolf state in "Optical coherence and quantum optics", that it is always pi/2. Hecht says something similar

 

[Alexander-1]

Semireflected (is this the right word?) mirrors won't work here as the phase difference between transmitted and reflected wave in such beam splitters is not pi, but pi/2. Modeling them as mirrors concerning the reflected part while doing nothing to the transmitted wave is not an appropriate description, which makes complete destructive interference impossible.

Maybe this is solution. A simple beamsplitter may be a very thin sheet of glass inserted in the beam at an angle to divert a portion of the beam in a different direction. This is so called http://www.redoptronics.com/beamsplitter-plate.html" because they have difficult metallic or dielectric coatings. I shall check your reference, but even simple metallic coating gives sophisticated phase shift. So, there is a sense to consider a simple model. For example, we can consider a plate of glass without any coatings as a beamsplitter. I shall try to make a calculation and hope to find the solution in this direction. I am sure that there is no waveguide effect in our case.

 

[lpfr]

Semireflected (is this the right word?) mirrors won't work here as the phase difference between transmitted and reflected wave in such beam splitters is not pi, but pi/2.

The correct word is semireflecting mirrors.

The limit conditions of EM waves on metallic surfaces imposes that, if the electric field is parallel to the surface, the reflected wave has a difference of phase of pi and the transmitted wave is in phase.
I do not see the origin of pi/2. When you look inside the reflection details, the phase of the wave created by the oscillating electrons in the metal is just in opposition (pi) with the incoming wave.
Metallic BS should work, but only for light polarized parallel to the metal. In the Alexander-1 drawing the light must be polarized perpendicular to the drawing.

Unfortunately we can not calculate the phase shift for http://www.directindustry.com/industrial-manufacturer/beamsplitter-78814.html" because they have difficult metallic or dielectric coatings..

Maybe you cannot modelize real BS. But you can always "build" a theoretical one.
Put, between the two prisms, a dielectric layer with a refraction index lower than the prisms. The thickness of the layer must satisfy the condition that the optical length of the light traversing the layer be an integer multiple of the wavelength. In fact there is another condition to take into account the multiple reflections, so the refraction index cannot really take any value. But this is secondary.

As the reflection on an interface with a lower refraction index inverses the phase (i.e. pi phase shift), the previous condition suffices to give zero output. You should do the drawing to see the situation.

Now, when you look at the wave vectors k in the layer, you will see that the vectors of the two waves add and give a no zero value in the direction of the diagonal (parallel to the layer). This is the direction where the power travels.

As I said in my previous (ignored) post, this is the same situation that you find in rectangular waveguides.

 

[Cthugha]

The limit conditions of EM waves on metallic surfaces imposes that, if the electric field is parallel to the surface, the reflected wave has a difference of phase of pi and the transmitted wave is in phase.
I do not see the origin of pi/2. When you look inside the reflection details, the phase of the wave created by the oscillating electrons in the metal is just in opposition (pi) with the incoming wave.

No. A good first start on why the difference in phase between reflected and transmitted wave is pi/2 is given in

A. C. Elitzur, L. Vaidman, Found. Phys. 23 (1993) 987-997

A better explanation is found in

P. D. Drummond, A. T. Friberg, J. Appl. Phys. 54 (1983) 5618-5625.

But this reference needs some prior knowledge concerning time reversal and em fields.

More elemental explanations can be found in

Z. Y. Ou, L. Mandel, Am. J. Phys. 57 (1989) 66-67.

or in the appendix of this pdf:

http://puhep1.princeton.edu/~mcdonald/examples/bunching.pdf"

The last reference offers some good further references to this topic.

 

[lpfr]

No. A good first start on why the difference in phase between reflected and transmitted wave is pi/2 is given in
A. C. Elitzur, L. Vaidman, Found. Phys. 23 (1993) 987-997
A better explanation is found in
P. D. Drummond, A. T. Friberg, J. Appl. Phys. 54 (1983) 5618-5625.
But this reference needs some prior knowledge concerning time reversal and em fields.
More elemental explanations can be found in
Z. Y. Ou, L. Mandel, Am. J. Phys. 57 (1989) 66-67.
or in the appendix of this pdf:
http://puhep1.princeton.edu/~mcdonald/examples/bunching.pdf"
The last reference offers some good further references to this topic.

I'm not able to treat more in detail the semireflecting metallic mirrors. I stick to dielectric BS.

Amid the lot of references inaccessible to me (I'm retired and I just have my personal books) that you gave, there was this one accessible:
http://puhep1.princeton.edu/~mcdonald/examples/optics/degiorgio ajp 48 81 80.pdf
Which gives a simple mathematical demonstration for lossless BS based on the conservation of energy and independent of the physical process. The basis of the demonstration is to say that outputs transport the same power as the inputs and implies that a situation as described in the drawing of Alexander-1 is impossible. It excludes the possibility that the energy could go elsewhere.
It is very funny that the other paper, also do the demonstration about the phase with two beams. Is there not a possibility to find the phase between the reflected and transmitted beam for just an incoming beam? Do you know of a demonstration about phases in a BS with just a beam?
As this experiment can be done with continuous and high power waves, instead of isolated photons or bunches of photons, an explanation with classical EM fields should be possible. When you use classical EM to find the phases with just one incoming beam, the classical limit conditions for EM fields, you do not find pi/2 but pi.
As we assume that all materials are linear, the behavior of each beam is independent of the presence of another one.
These are the classical EM formulas for reflected and transmitted amplitudes at the interface between two dielectrics (for waves polarized parallel to the interface):
{E_r \over E_i}={ n_1\cos \theta_i - n_2\cos \theta_t \over n_1\cos \theta_i + n_2\cos \theta_t}
{E_t \over E_i}={2n_1\cos\theta_i\over n_1\cos \theta_i + n_2\cos \theta_t}
As you can see the transmitted wave is always in phase, and the reflected wave is either in phase or in opposition of phase. Nowhere is a pi/2.
Would you say that they that these formulas are false or that they do not apply when there are two beams?

 

[Cthugha]

I would say, these formulas are right.
This kind of Fresnel's formula holds true at the interface between two dielectrics. That means that the two beams propagate in different dielectrics after hitting the beam splitter.

Usual beam splitters (the same dielectric before and after the beam splitter) usually need a certain thickness to enable constructive interference between the reflections from both edges to occur. So a beam splitter should show a length (or better optical path) of lambda/4, so that the phase shift of pi, which happens by reflection at the first edge is canceled by the phase shift due to the longer propagation time in the second dielectric.
So there is a phase difference of pi/2 between transmitted and reflected wave due to the longer path of lambda/4.

Anyway, do not quote me on that. I do not know much about beam splitters and just used them to trigger photo diodes so far. I never really had a closer look on them.

 

[lpfr]

Usual beam splitters (the same dielectric before and after the beam splitter) usually need a certain thickness to enable constructive interference between the reflections from both edges to occur. So a beam splitter should show a length (or better optical path) of lambda/4, so that the phase shift of pi, which happens by reflection at the first edge is canceled by the phase shift due to the longer propagation time in the second dielectric.
So there is a phase difference of pi/2 between transmitted and reflected wave due to the longer path of lambda/4.

Constructive interference between multiple reflections asks for the good thickness of the layer.
But the path difference is a function of the angle \theta_t and there is very small chances for it to be a rational factor of lambda (you must make the drawing to see this).
Even if you must add a layer to satisfy constructive interferences, you can choose the refraction index to have any phase difference, and not just pi/2.

This leaves unanswered the question of Alexander-1, if my explanation is not the good one.

 

[Alexander-1]

I would say, these formulas are right.
This kind of Fresnel's formula holds true at the interface between two dielectrics. That means that the two beams propagate in different dielectrics after hitting the beam splitter.

Usual beam splitters (the same dielectric before and after the beam splitter) usually need a certain thickness to enable constructive interference between the reflections from both edges to occur. So a beam splitter should show a length (or better optical path) of lambda/4, so that the phase shift of pi, which happens by reflection at the first edge is canceled by the phase shift due to the longer propagation time in the second dielectric.
So there is a phase difference of pi/2 between transmitted and reflected wave due to the longer path of lambda/4.

Thanks for your link, which is very useful and give a key to solution of the problem. It seems the phase shift in the beamsplitter is really do not equal to pi. For me it is still not clear why (sorry, I did not understood your explanations), but following the links in your article I think I can find the mechanism of this phenomena.

 

[Alexander-1]

This leaves unanswered the question of Alexander-1, if my explanation is not the good one.

What is your explanation? Metal/dielectric coating acts as a waveguide? What can I say.. Maybe yes, maybe no.. Formulas are required. In any case I can not agree that power is lost at the BS (producers of BS would not allow this).

 

[lpfr]

What a think is that the power is "pushed" along the diagonal by the incoming beams. It is not really guided as in a waveguide. At the edges of the beams the light exits. If the beams cover al the BS, the power will exit at the edge of the cube.
I never said that power was lost or absorbed in the BS.

 

[Cthugha]

Constructive interference between multiple reflections asks for the good thickness of the layer.
But the path difference is a function of the angle \theta_t and there is very small chances for it to be a rational factor of lambda (you must make the drawing to see this).

Oh, sorry. What I tried to say was possibly not clear.
The path difference is of course a function of the angle. But if you consider reflections at both edges, the transmittivity and reflectivity should depend on the angle as well.
If the path difference is not a rational factor of lambda, I don't think that a 50:50 beam splitter ratio is even possible.
It is not clear to me, how there could be an arbitrary phase difference, if interferences are supposed to occur.

For thin dielectric interfaces however, the approach you presented should hold true.

 

[Manchot]

The reason that the phase shift isn't simply pi is because the mirrors cannot possibly be composed of perfect conductors. If they were, then they would reflect all of their incident light!

 

[Claude Bile]

The key here I think is to consider polarisation effects. For the blue and red beams (referring to the image in the original post), the reflected and transmitted beams will have different polarisations.

Needless to say, if the polarisation of the reflected and transmission components are different, the combined beams will not be 0, even if they are 180 degrees out of phase.

Claude.

 

[Alexander-1]

For the blue and red beams (referring to the image in the original post), the reflected and transmitted beams will have different polarisations.

No, polarizations are the same. Reflection does not change the state of polarization.

 

[Alexander-1]

The reason that the phase shift isn't simply pi is because the mirrors cannot possibly be composed of perfect conductors. If they were, then they would reflect all of their incident light!

What is the "perfect conductors"? Thin dielectric or metal layer will reflect a part of radiation. Other part will transmit. In theory and in experiment. Even simple glass surface will reflect the part of radiation.

 

[Alexander-1]

Oh, sorry. What I tried to say was possibly not clear.
The path difference is of course a function of the angle. But if you consider reflections at both edges, the transmittivity and reflectivity should depend on the angle as well.
If the path difference is not a rational factor of lambda, I don't think that a 50:50 beam splitter ratio is even possible.
It is not clear to me, how there could be an arbitrary phase difference, if interferences are supposed to occur.

For thin dielectric interfaces however, the approach you presented should hold true.

You said about "reflections at both edges".. What edges? If we consider "Beamsplitter Plate" (semireflecting mirorr), then the glass plate is covered by reflecting metal or dielectric coating from one side, while the other side is covered by an anti-reflection coating. So reflection occurs just at one side of the plate. In cubic splitter two right-angle prisms are cemented together at their hypotenuse faces; one of such faces are covered by reflecting layer. So there is no two edges too.

 

[lpfr]

The reason that the phase shift isn't simply pi is because the mirrors cannot possibly be composed of perfect conductors. If they were, then they would reflect all of their incident light!

I do not know what you understand by "perfect conductors". Anyhow, if you have a conductor without ohmmic losses, but with few free electrons, the wave created by the oscillating electrons will not have the amplitude needed to "reflect" totally the incoming wave. But even in this case, the phase of the oscillating electrons and of the generated wave is the same. It is not because there are few electrons that their phase changes.

On the other hand, you do not need to stick to metallic BS. You can use dielectric BS. And this time your argument can be discarded.