You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Bernoulli equation application
- Thread starter Chemist@
- Start date
AI Thread Summary
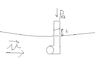
The water level in the object is higher than in the current due to the pressure generated by the current's velocity. According to Bernoulli's equation, the relationship between velocity, pressure, and height determines the water level. A faster current velocity leads to increased pressure, allowing water to rise higher in the object. The equation suggests that any velocity will elevate the water level in the pipe, as the pressure differential is sufficient to counteract gravity. Understanding these principles is essential for applying Bernoulli's equation accurately in this scenario.
Physics news on Phys.org
The_Engineer
- 17
- 0
The water level in the object is above the water level in the current because the current is supplying enough pressure to push the water that high. The current has a velocity, and you can probably imagine that faster velocity entails a higher water level in the object. There is also a distance involved, which is the height of the fluid in the object. Velocity, pressure, and distance are all part of Bernoulli's equation.
Chemist@
- 115
- 1
I know all that, but how would the equation look like in this case.
russ_watters
Mentor
- 23,694
- 11,136
It's the standard/most common form of the equation. Have you looked it up?
Chemist@
- 115
- 1
I know the standard form. What must be the velocity so that the water level in the object is above the normal level? Is it: V>sqrt(2pa/ro)
russ_watters
Mentor
- 23,694
- 11,136
For your sketch, any velocity will cause the water level in the pipe to rise.
Chemist@
- 115
- 1
Could you please elaborate why?
Similar threads
- Replies
- 4
- Views
- 2K
- Replies
- 19
- Views
- 3K
- Replies
- 2
- Views
- 3K
- Replies
- 11
- Views
- 3K
- Replies
- 2
- Views
- 1K
- Replies
- 30
- Views
- 2K
- Replies
- 4
- Views
- 3K
- Replies
- 1
- Views
- 2K
- Replies
- 12
- Views
- 3K
- Replies
- 47
- Views
- 4K
Hot Threads
-
I Explain Bernoulli at the molecular level?
- Started by user079622
- Replies: 251
- Classical Physics
-
B Simple mass/scale puzzle
- Started by DaveC426913
- Replies: 206
- Classical Physics
-
I Solving a momentum problem where masses change after the collision
- Started by rdemyan
- Replies: 35
- Classical Physics
-
I Topic about physics axioms, theory, laws etc..
- Started by user079622
- Replies: 93
- Classical Physics
-
I Two kinds of pressure
- Started by Demystifier
- Replies: 24
- Classical Physics
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 5
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 11
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math