Blocks sliding down different lengths of ramp

[dibilo]

I have been watching videos on the brachistochrone curve and from my understanding, the curve works as the ball goes through more acceleration at start, therefore causing it to reach the end the fastest. However, I understand that acceleration towards Earth is constant (9.81 m/s^2) and this brings me to another question.

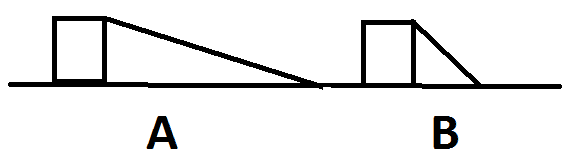
From experience, I believe that if I slide a block down both ramps from the same height, a block will reach the ground faster on ramp B than ramp A. Since acceleration towards Earth is constant, what caused the difference in timing? Is it just friction?

Thanks for your help in advance!

 

[kuruman]

From experience, I believe that if I slide a block down both ramps from the same height, a block will reach the ground faster on ramp B than ramp A

It's not friction. It's the component of the acceleration of gravity in the vertical direction that counts. Think of doing this on a frictionless ramp. When the angle of the incline is zero, the time is infinite, because there is no acceleration in the vertical direction and the block once at rest, stays at rest. When the angle of the ramp is 90^o, the time is a minimum because the acceleration is as large as it would get for any angle, namely the acceleration of gravity, and the block is in free fall.

On edit: The component of the acceleration of gravity along the ramp is a_x = g sinθ, where θ is the angle with respect to the horizontal.

 

[JRMichler]

What kuruman said. In addition, shallower angles have longer ramps. The result is that shallower ramps have both lower acceleration and longer distance to travel.

 

[lekh2003]

The first issue with your assumption is that acceleration is constant when going down a slope. Brachistocrone curves do not have constant slopes and therefore do not have constant acceleration.

Acceleration due to gravity = g sin (theta). The acceleration due to gravity is different due to different slopes. With steep slopes as in Ramp B, theta approaches 90 degrees and the acceleration approaches 9.8 m/s^2. With Ramp A, theta is quite small, and the acceleration due to gravity on the slope is just a fraction of the actual acceleration due to gravity. Ramp B will accelerate an object faster.

A Brachistocrone curve resembles the ideal changing slope for an object to accelerate down. If you wanted to calculate the actual Brachistochrone curve, we could get into some serious calculus.

My suggestion is that you study forces and their effects a little more and then look at Brachistochrone curve videos. The basic reason behind all this is the changing acceleration due to a changing slope (not friction).