- #1
Phrak
- 4,267
- 6
It seems that Bode published Titius' discovery without crediting Titius, so I will call it Titius' Rule.
Titius' Rule, in it's modern adaption, says there is a geometric progression in the distance the planets circle the Sun. It's not a perfect rule, and Neptune doesn't fit at all. However, the astroid belt serves in place of planet 5, and Pluto serves for planet number 9.
The pendulum of controversy has swung back and forth a bit. Is it meaningful, or happenstance?
Apparently this topic hasn't been discussed on physicsforum since 2004 [edit: 2008], and in the mean time we now have data from observations of other solar systems.
This article has a nice graph of data made available 2 months ago.
http://www.economist.com/blogs/babbage/2010/08/planet_hunting"
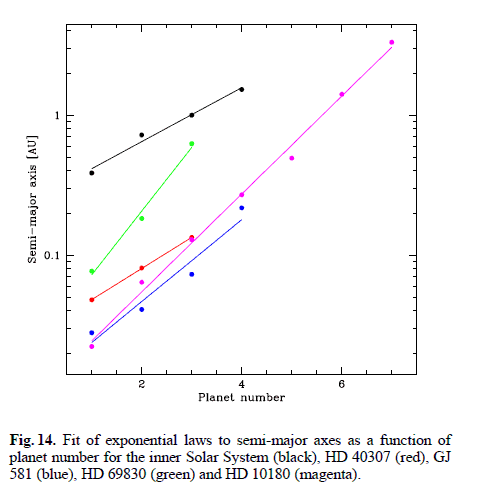
Titius' Rule in modern form is
[tex] ln(a) = mN+b \ .[/tex]
'a' is the semimajor axis of planet number 'N'. 'm' and 'b' are constants chosen for best fit curve.
I tend to imagine that this orbital spacing is the most stable. For orbits to be stable we can't have orbital periods in simple ratios or perturbations would accumulate with each realignment of two planets until the arrangement blew itself up. I suspect this geometric relationship must somehow minimized gravitational harmonic coupling.
With C, a constant, the orbital period is
[tex]T = C a^{3/2} \ .[/tex]
This leads to the same sort of equation, but in T.
[tex]ln(T) = cN+d[/tex]
Cleaned up a little, we can write
[tex]e^N = k(T/T_0) \ .[/tex]
Is this planetary spacing the most stable?
Titius' Rule, in it's modern adaption, says there is a geometric progression in the distance the planets circle the Sun. It's not a perfect rule, and Neptune doesn't fit at all. However, the astroid belt serves in place of planet 5, and Pluto serves for planet number 9.
The pendulum of controversy has swung back and forth a bit. Is it meaningful, or happenstance?
Apparently this topic hasn't been discussed on physicsforum since 2004 [edit: 2008], and in the mean time we now have data from observations of other solar systems.
This article has a nice graph of data made available 2 months ago.
http://www.economist.com/blogs/babbage/2010/08/planet_hunting"
Titius' Rule in modern form is
[tex] ln(a) = mN+b \ .[/tex]
'a' is the semimajor axis of planet number 'N'. 'm' and 'b' are constants chosen for best fit curve.
I tend to imagine that this orbital spacing is the most stable. For orbits to be stable we can't have orbital periods in simple ratios or perturbations would accumulate with each realignment of two planets until the arrangement blew itself up. I suspect this geometric relationship must somehow minimized gravitational harmonic coupling.
With C, a constant, the orbital period is
[tex]T = C a^{3/2} \ .[/tex]
This leads to the same sort of equation, but in T.
[tex]ln(T) = cN+d[/tex]
Cleaned up a little, we can write
[tex]e^N = k(T/T_0) \ .[/tex]
Is this planetary spacing the most stable?
Last edited by a moderator: