BRS: Using geodesic congruences and frame fields to compute optical experience

[Chris Hillman]

I. Overview

Another SA asked me to elaborate on a remark I made to the effect that frequency shift phenomena always (even in Minkowski vacuum) involve at least the following ingredients:

• two (proper time parameterized) timelike curves C, C'
• an event A on C ("emission event")
• an (affinely parameterized) null geodesic C'' from A to an event A' on C' ("reception event").

Notice that once A is chosen, in the case of a curved spacetime, it is possible that several null geodesics from A intersect C' at various different reception events, which is one reason why "distance in the large" is so tricky even if defined by the simplest method, radar distance.

Given these ingredients, one can compute a energy-momentum four-vector all along C'', representing a "photon" whose world line is C''. Then by taking the inner product of this four-vector at A with the unit tangent vector to C and comparing with the inner product at A' with the unit tangent vector to C', one can compute "photon energy" (or equivalently, frequency or wavelength) at the emission and reception events.

In simple cases, one can often make a reasonable decomposition of the net frequency shift into a kinematic Doppler shift and a gravitational frequency shift, but one should not expect this to be feasible or even insightful in every case.

 

[Chris Hillman]

[EDIT: After posting this as part II, I realized it should be part III, with part II discussing Minkowski vacuum.]

Consider next the standard Schwarzschild chart on the exterior of the Schwarzschild vacuum solution:
<br /> \begin{array}{rcl}<br /> ds^2 &amp; = &amp; -(1-2m/r) \; dt^2 + \frac{dr^2}{1-2m/r} + r^2 \; d\Omega^2 \\<br /> &amp;&amp; 2m &lt; r &lt; \infty<br /> \end{array}<br />
That is, we have the metric tensor
<br /> \left[ \begin{array}{cccc}<br /> -(1-2m/r) &amp; 0 &amp; 0 &amp; 0 \\<br /> 0 &amp; 1/(1-2m/r) &amp; 0 &amp; 0 \\<br /> 0 &amp; 0 &amp; r^2 &amp; 0 \\<br /> 0 &amp; 0 &amp; 0 &amp; r^2 \, \sin(\theta)^2<br /> \end{array} \right]<br />
which can use to compute the inner product, in the tangent space to some event E, of any two vectors at E.

We would like to compute the frequency shift of light from "the distant fixed stars" as observed by various observers in our spacetime. To do this we need the general ingoing null geodesic congruence. In previous posts I showed how by solving the Killing equation to obtain four independent Killing vector fields we can use Noetherian magic to obtain four first integrals. The result is the null geodesic congruence
<br /> \begin{array}{rcl}<br /> \vec{k} &amp; = &amp; \frac{E}{1-2m/r} \, \partial_t - \sqrt{E^2-V} \, \partial_r<br /> + \frac{1}{r^2} \; \left( \sqrt{L^2-J^2/\sin(\theta)^2} \, \partial_\theta <br /> + \frac{J}{\sin(\theta)^2} \, \partial_\phi \right) \\<br /> &amp;&amp; V = \left( 1 - \frac{2m}{r} \right) \; \frac{L^2}{r^2}<br /> \end{array}<br />
More properly, the geodesics which make up the congruence are the integral curves of this null geodesic vector field. To find an integral curve, read off the corresponding system of first order ODEs in which t,r,\theta, \phi are treated as functions of the parameter \lambda:
<br /> \begin{array}{rcl}<br /> \dot{t} &amp; = &amp; \frac{E}{1-2m/r} \\<br /> \dot{r} &amp; = &amp; - \sqrt{E^2-(1-2m/r) \; L^2/r^2} \\<br /> \dot{\theta} &amp; = &amp; \frac{1}{r^2} \; \left( \sqrt{L^2-J^2/\sin(\theta)^2} \\<br /> \dot{\phi} &amp; = &amp; \frac{J}{r^2 \, \sin(\theta)^2}<br /> \end{array}<br />
Now choose initial values for the coordinates (specifying the event we start the curve from) and solve this system. To be sure, this injunction may not be so easy to carry out, but fortunately, we often do not really need the equations giving the geodesic itself as an affinely parameterized curve, just the tangent vector at some event on this curve.

Letting r tend to infinity, we see that E represents the energy of the photon as measured by "a static observer at r=infty", a claim which is to be understood as shorthand for a limiting process. One can argue that it in some sense L is the angular momentum about the origin, as measured by said "observer", but this is trickier. But whatever their physical interpretation, it is clear that E, L, J are constants of motion and they determine the initial direction of the integral curve in the initial value problem just described. In particular, we can start at some event on the world line of some observer and propagate backwards in time the null geodesic through that event which starts off in some direction given by E, L, J.

Incidentally, it often helps to be a bit loose about the distinction between a single geodesic curve and an entire geodesic congruence. Even if we are only interested in a single geodesic, it is often helpful to regard it as one member of an entire congruence and then to apply machinery for computing with congruences. This is particularly convenient when using NP formalism because then often one of the two real vector fields in our NP tetrad has integral curves which are affinely parameterized null geodesics (and if so, the NP spin coefficients give essentially the same information as the optical scalar, the test for whether a null curve is an affinely parameterized null geodesic, and so forth). Bearing this in mind, we can think of the energy and specific angular momenta parameters as belonging to a single photon (or a small wave packet in classical terms) or as defining a congruence all of whose members share the same first integrals (constants of motion).

Similarly, when we model the world line of an ideal observer using some timelike curve, it is often convenient to think of it as one member of an entire congruence of timelike curves.

The "Noetherian magic" method guarantees that we will come up with an affinely parameterized null geodesic vector field, which we can then integrate with suitable initial values (the components yield a system of first degree ODEs) to obtain a specific geodesic in the congruence. But if we didn't already know that \vec{k} is an affinely parameterized null geodesic vector field, we could compute the covector
<br /> k_{a ;b} \; k^b<br />
This is a scalar multiple of the covector k_a iff k defines a null geodesic congruence, and vanishes entirely iff the geodesics are also affinely parameterized.

It is often best to rewrite this vector field in terms of E and the specific angular momenta
<br /> \tilde{L} = L/E, \; \tilde{J} = J/E<br />
(where L is the total magnitude of the angular momentum and J is the component corresponding to motion in the equatorial plane). In the equatorial plane \theta=\pi/2 we obtain:
<br /> \begin{array}{rcl}<br /> \vec{k} &amp; = &amp; E \; \left( \frac{1}{1-2m/r} \, \partial_t <br /> - \sqrt{1-\tilde{V}} \, \partial_r<br /> + \frac{1}{r^2} \; \left( \sqrt{\tilde{L}^2-\tilde{J}^2} \, \partial_\theta <br /> + \tilde{J} \, \partial_\phi \right) \right) \\<br /> &amp;&amp; \tilde{V} = \left( 1 - \frac{2m}{r} \right) \; \frac{\tilde{L}^2}{r^2}<br /> \end{array}<br />
Then we see that the entire vector is scalar multiplied by the energy E and the trajectory (relative sizes of the components) depends only on the specific angular momenta. This is why there is (in the geodesic optics approximation) no colored fringes due to gravitational lensing: all frequencies of photons bend the same way.

Notice that \dot{r} = 0 (derivative wrt the affine parameter) when \tilde{V}=1, or at r=b where b is a positive real solution of
<br /> b^3 = (b-2m) \; \tilde{L}^2 <br />
This shows how the total specific angular momentum L relates to the impact parameter b. That is, restricting attention to the far field, a photon typically comes in from r=infinity, reaches a minimum r=b, then zooms back out in a slightly different asymptotic direction (light bending). Closer in, where the field is stronger, it might wind several times around the horizon before zooming back out, or it might fall past the event horizon into the future interior region (in which case it will never re-emerge).

Notice that the case L=J is the case in which the photon moves in the equatorial plane. If L^2 > J^2, then it is moving in another plane "through the origin", but here we are only interested in what happens when it intersects a timelike curve which lies in the equatorial plane.

The idea here is that for a given observer's world line, at equal intervals of proper time we can in principle trace null geodesics backwards in time to some fixed star, and then we'll apply our setup to "the static observer at r = infty" corresponding to that fixed star, to the particular null geodesic we found, and to the world line of the observer whose optical experience we wish to study.

The proper time parameterized timelike curve which is the world line of a static (non-inertial!) observer at r=r_0 is the integral curve of the timelike (non-geodesic!) unit vector field:
<br /> \vec{u} = \frac{1}{\sqrt{1-2m/r_0}} \; \partial_t<br />
Taking the inner product (and remembering that we are working with -+++ signature) we have
<br /> -\vec{u} \cdot \vec{k} = \frac{E}{\sqrt{1-2m/r_0}}<br /> \approx E \; \left( 1 + m/r_0 \right) + O \left( 1/r_0^2 \right)<br />
This is larger than E, so we have a blue shift. Obviously we expect a blue shift ("pure gravitational blue shift") for a radially falling photon which reaches our static observer, and because he is "not moving wrt the fixed stars" we expect that we get the same result for light coming from any other direction. Which is of course what we just verified.

Notice that I didn't actually choose a specific observer's world line, and I certainly didn't exhibit a specific null geodesic which intersects that world line. I just assumed that the parameters E, L,J have been chosen so that we do have some null geodesic interesecting some event on the some static observer's world line.

For a more interesting example, consider the Hagihara observer at r=r_0 (where r_0 > 6m). Recall that these are the observers who move in stable circular orbits in the exterior region. The proper time parameterized timelike curve which is the world line of a Hagihara observer at r=r_0 is the integral curve of the timelike unit vector field
<br /> \vec{u} = \frac{1}{\sqrt{1-3m/r_0}} \; \partial_t<br /> + \frac{\sqrt{m/r_0^3}}{\sqrt{1-3m/r_0}} \; \partial_\phi<br />
(in the equatorial plane). Now we obtain (in the equatorial plane)
<br /> -\vec{u} \cdot \vec{k} = E \; \frac{1-\sqrt{\frac{m}{r_0^3}} \, \tilde{J}}{\sqrt{1-3m/r_0}} <br /> \approx E \; \left( 1 + \frac{3m}{2r_0} - \sqrt{\frac{m}{r_0^3}} \tilde{J} \right)<br /> + O \left( 1/r_0^2 \right)<br />
Notice this depends on the sign of the specific angular momentum! Thus, for sufficiently small \tilde{J} and sufficiently large r_0, the gravitational blue shifting of the falling photon dominates any frequency shift due to the motion of the Hagihara observer, but under some circumstances, a photon which approaches the moving observer "from behind" might actually arrive red shifted rather than blue shifted. And if
<br /> \frac{ 1 - \sqrt{\frac{m}{r_0^3}} \, \tilde{J} }{\sqrt{1-3m/r_0}} = 1<br />
the kinematic red shift and gravitational blue shift exactly cancel, so to speak.

We could factor
<br /> \frac{ 1 - \sqrt{\frac{m}{r_0^3}} \, \tilde{J} }{\sqrt{1-3m/r_0}} =<br /> \frac{1}{\sqrt{1-2m/r_0}} \; \frac{\sqrt{1-2m/r_0}}{\sqrt{1-3m/r_0}} \;<br /> \left( 1 - \sqrt{\frac{m}{r_0^3}} \; \tilde{J} \right)<br />
and since we already identified the first factor here as the pure gravitational blue shift of a falling photon, we could try to argue that the product of the remaining factors represents the kinematic or Doppler shift. I am not sure this is really worth the trouble, however!

Recall that the Lemaitre observers fall "from rest at r=infty", freely and radially. The world line of such an observer is an integral curve of the unit timelike vector field
<br /> \vec{u} = \frac{1}{1-2m/r} \; \partial_t - \sqrt{\frac{2m}{r}} \; \partial_r<br />
(Notice that this expression is only valid for the portion of the world line which lies in the exterior region!) Now we obtain
<br /> -\vec{u} \cdot \vec{k} = <br /> \frac{E}{1-2m/r} \; \left( 1 - \sqrt{\frac{2m}{r}} \;<br /> \sqrt{1 - \tilde{V} } \right)<br />
Notice that this depends on \tilde{L}[/tex] but is independent of \tilde{J}. Recalling that the Lemaitre observer is falling in radially, and that the spacetime is symmetric under rotation about any radius (so to speak), it makes sense that this should be the case. (But this would not be true in Kerr vacuum, for example!)<br /> <br /> By the same method of Noetherian magic, we can find the tangent vector to the world line of an arbitrary infalling observer. Then our inner product will contain the energy/momenta of both the observer and the photon. However, because infalling observers only spend some portion of their history in the exterior region, it makes sense at this point to switch to a chart in which we an follow the history of infalling observers through the event horizon and into the future interior region. The simplest such chart is the ingoing Eddington chart<br /> &lt;br /&gt; \begin{array}{rcl}&lt;br /&gt; ds^2 &amp;amp; = &amp;amp; -(1-2m/r) du^2 + 2 \, du \, dr + r^2 \, d\Omega^2 \\&lt;br /&gt; &amp;amp;&amp;amp; 0 &amp;lt; r &amp;lt; \infty\&lt;br /&gt; \end{array}&lt;br /&gt;<br /> which can be obtained from the Schwarwzschild chart by putting<br /> &lt;br /&gt; du = dt + \frac{dr}{1-2m/r}&lt;br /&gt;<br /> and then extending the range from 2m &amp;lt; r &amp;lt; \infty to 0 &amp;lt; r &amp;lt; \infty, which is acceptable in the new chart because the coordinate singularity at the event horizon is removed in these coordinates. This chart covers the exterior and future interior regions.<br /> <br /> By Noetherian magic, the general ingoing (affinely parameterized) null geodesic is given (in the equatorial plane) by<br /> &lt;br /&gt; \begin{array}{rcl}&lt;br /&gt; \vec{k} &amp;amp; = &amp;amp; E \; \left( \frac{1-\sqrt{1-\tilde{V}}}{1-2m/r} \, \partial_t &lt;br /&gt; - \sqrt{1-\tilde{V}} \, \partial_r&lt;br /&gt; + \frac{1}{r^2} \; \left( \sqrt{\tilde{L}^2-\tilde{J}^2} \, \partial_\theta &lt;br /&gt; + \tilde{J} \, \partial_\phi \right) \right) \\&lt;br /&gt; &amp;amp;&amp;amp; \tilde{V} = \left( 1 - \frac{2m}{r} \right) \; \frac{\tilde{L}^2}{r^2}&lt;br /&gt; \end{array}&lt;br /&gt;<br /> <br /> The timelike unit vector field whose integral curves are the world lines of the Lemaitre observers becomes, in this chart<br /> &lt;br /&gt; \vec{u} = \frac{1}{1 + \sqrt{\frac{m}{r}}} \; \partial_u&lt;br /&gt; - \sqrt{\frac{2m}{r}} \; \partial_r&lt;br /&gt;<br /> We find<br /> &lt;br /&gt; -\vec{v} \cdot \vec{k} = E \; \frac{1-\sqrt{\frac{2m}{r}} \; \sqrt{1-\tilde{V}}}{1-2m/r} &lt;br /&gt;<br /> which agrees with our previous result, as must happen. Recalling that<br /> &lt;br /&gt; \tilde{V} = \left(1- \frac{2m}{r} \right) \; \frac{\tilde{L}}{r^2}&lt;br /&gt; <br /> note that small values of \tilde{L} correspond to null geodesics with small impact parameters, i.e. which are close to a radial half-line. Then if we plug in some values and plot the frequency shift, we find that initially the red shift due to the fact that the observer is falling away from the distant star and towards the Schwarzschild object dominates the gravitational blue shift due to the fact that the photon is also falling towards that object. But at some small radius, this is rather suddenly converted to blue shifting which rapidly diverges as our Lemaitre observer approaches r=0 (the locus of the strong spacelike curvature singularity). For larger values of \tilde{L}, we will typically find that we have two distinct geodesics, one living on the asympotically flat exterior sheet and one which plunges into the hole, separated by a region where no geodesics with the specified parameters exist (as real curves).<br /> <br /> (&quot;Schwarzschild object&quot;: the source of the field could be a black hole or it could be nonrotating star with the same mass. Even in the second case, the outgoing Eddington chart has many advantages, but the ingoing Eddington chart is useful mainly for studying infall into a black hole.)<br /> <br /> A special case of particular interest arises when the infalling photon has L=0, i.e. it is falling in radially and catches up with the (subluminal!) Lemaitre observer. Then we have<br /> &lt;br /&gt; -\vec{u} \cdot \vec{k} = E \; \frac{1-\sqrt{\frac{2m}{r}}}{1-2m/r} &lt;br /&gt; = E \; \frac{1}{1+\sqrt{\frac{2m}{r}}}&lt;br /&gt;<br /> This shows that the photon always arrives redshifted: the &quot;kinematic&quot; effect of the observer falling away from the star dominates the &quot;gravitational&quot; effect due to the fact that photon is also falling. Furthermore, as r tends to 0 from above, it is infinitely redshifted. But, as already remarked earlier, if the photon has even a small angular momentum, eventually the redshift is converted to blueshift.<br /> <br /> Another interesting class of (non-inertial!) observer are the slowfall observers, who accelerate radially outward with just enough thrust to maintain their position according to Newtonian theory, but because gravity gravitates in gtr, they slowly fall into the hole in our gtr model. The timelike unit vector field whose integral curves define a congruence of world lines of slowfall observers is<br /> &lt;br /&gt; \vec{u} = \partial_u - \frac{m}{r} \; \partial_r&lt;br /&gt;<br /> This gives<br /> &lt;br /&gt; -\vec{u} \cdot \vec{k} = E \; \frac{ 1-\frac{m}{r} \; &lt;br /&gt; \left( 1 + \sqrt{1-\tilde{V}} \right) }{1-2m/r}&lt;br /&gt;<br /> The slowfall observers are falling in radially (but not inertially), so we should expect this to depend only on the total specific angular momentum, and it does. For both the Lemaitre and slowfall observers, the frequency shift depends only on the magnitude of \tilde{L}, not its sign, which is again explicable on the grounds of symmetry.<br /> <br /> Yet another interesting class of observers are the Frolov observers, whose entire history is located inside the event horizon (the ingoing Eddington chart only covers the future half of their histories). The timelike unit vector field whose integral curves define a congruence of world lines of Frolov observers is<br /> &lt;br /&gt; \vec{u} = \frac{1}{\sqrt{2m/r-1}} \; \partial_u - \sqrt(2m/r-1} \; \partial_r,&lt;br /&gt; \; \; 0 &amp;lt; r &amp;lt;2m&lt;br /&gt;<br /> Then<br /> &lt;br /&gt; -\vec{u} \cdot \vec{k} = E \; \frac{\sqrt{1-\tilde{V}}}{\sqrt{2m/r-1}}&lt;br /&gt;<br /> <br /> Specialized charts can be very useful in studying the question of the optical appearance of the sky as seen by some observer. Some 15 years ago, in a sci.physics post, I described how the Costa chart can be used to study strong gravitational lensing. This chart covers only the exterior region, and (with one angular coordinate suppressed) we can plot the geodesics on a cylinder rather than a plane, and then we can cut the cylinder and unwrap it to plot them without intersections. This can be very useful in seeing how strong lensing works. The result is a rather vivid picture of primary, secondary, tertiary images which together outline the &quot;dark disk&quot;. This is not the horizon, which is of course invisible, but an optical illusion due to the strong lensing and in particular the tendency of null geodesics which approach too close to the horizon to suddenly turn and plunge right in.<br /> <br /> Next up: pictures and more detailed discussion.

 

[Dale]

Hi Chris, thanks for working this out.

In the equatorial plane \theta=\pi/2 we obtain:
<br /> \begin{array}{rcl}<br /> \vec{k} &amp; = &amp; E \; \left( \frac{1}{1-2m/r} \, \partial_t <br /> - \sqrt{1-\tilde{V}} \, \partial_r<br /> + \frac{1}{r^2} \; \left( \sqrt{\tilde{L}^2-\tilde{J}^2} \, \partial_\theta <br /> + \tilde{J} \, \partial_\phi \right) \right) \\<br /> &amp;&amp; \tilde{V} = \left( 1 - \frac{2m}{r} \right) \; \frac{\tilde{L}^2}{r^2}<br /> \end{array}<br />
Then we see that the entire vector is scalar multiplied by the energy E and the trajectory (relative sizes of the components) depends only on the specific angular momenta.

So in this case k is in fact the four-momentum of the null particle. Is that true in general or only in specific spacetimes (e.g. static or stationary)? Also, I clearly see how it is scalar multiplied by E, but I don't clearly see how the remaining part is automatically correctly normalized.

PS you missed a 1/r² factor on \dot{\phi}

 

[Chris Hillman]

PS you missed a 1/r² factor on \dot{\phi}

Thanks! I just corrected that.

So in this case k is in fact the four-momentum of the null particle.

Mathematically speaking, in terms of the theory of smooth manifolds, it's the wave vector field for a null geodesic congruence, which consists of non-intersecting null geodesics filling up an open set in the spacetime. Each null geodesic curve in the congruence is affinely parameterized and its tangent vectors along the curve are the vectors assigned to that event by the vector field k. (The smooth structure underlies the Lorentzian structure on our spacetime model.)

Physically speaking, if we think of a given null geodesic curve as "the world line of a photon" as in Taylor & Wheeler, with Minkowski spacetime replaced by a curved spacetime, then each vector given by k at some event along the curve should correspond to the energy-momentum four-vector, which is null as it should be. Since the Lorentzian structure guarantees that at the level of a tangent space, everything should work just like in special relativity, this interpretation seems secure at a given tangent space. What we need to do here is to extend that to connect the interpretations at two different tangent spaces.

Similarly for timelike geodesics.

Mathematically, if we have a geodesic we obtain the tangent vectors by differentiation. If we use a proper time parameterization for a timelike geodesic (special case of an affine parameterization), it is pretty obvious that this is what we need to connect two tangent space interpretations. In this case, an affine parameter other than the proper time parameter will be a constant nonzero scalar multiple of the proper time parameter (the same scalar all along the curve). In the case of null geodesics, the best we can do is an affine parameterization, but that's good enough.

For many questions about null geodesics, we can consider a sequence of timelike geodesics which we argue approaches the null geodesic in a suitable sense. Some authors use this approach to show that for null curves, an affine parameter is just good enough to play the role played by proper time parameter for a timelike curve. This leaves stuff defined only up to a constant scalar multiple. In this case we are comparing ratios (energies measured at emission and reception events in appropriate frames at those events).

(I don't think I'm explaining this very well...)

Is that true in general or only in specific spacetimes (e.g. static or stationary)?

The general setup and the somewhat obscure remarks in the paragraphs just above should hold generally.

Also, I clearly see how it is scalar multiplied by E, but I don't clearly see how the remaining part is automatically correctly normalized.

I did two things when I rewrote
<br /> \begin{array}{rcl}<br /> \vec{k} &amp; = &amp; \frac{E}{1-2m/r} \, \partial_t - \sqrt{E^2-V} \, \partial_r<br /> + \frac{1}{r^2} \; \left( \sqrt{L^2-J^2/\sin(\theta)^2} \, \partial_\theta <br /> + \frac{J}{\sin(\theta)^2} \, \partial_\phi \right) \\<br /> &amp;&amp; V = \left( 1 - \frac{2m}{r} \right) \; \frac{L^2}{r^2}<br /> \end{array}<br />

• I pulled out the scalar E
• I specialized to the equatorial plane \theta=\pi//2, which makes \sin(\theta)=1

So with
<br /> \begin{array}{rcl}<br /> \tilde{L} &amp; = &amp; L/E \\<br /> \tilde{J} &amp; = &amp; J/E \\<br /> \tilde{V} &amp; = &amp; V/E^2 = (1-2m/r) \; \frac{\tilde{L^2}}{r^2}<br /> \end{array}<br />
we have

• t component (obvious)
• r component
  <br /> \sqrt{E^2-V} = E \; \sqrt{1-\tilde{V}}<br />
• \theta component
  <br /> \frac{1}{r^2} \; \sqrt{L^2-J^2/\sin(\theta)^2} =<br /> E \; \frac{1}{r^2} \; \sqrt{\tilde{L}^2-\tilde{J}^2/\sin(\theta)^2}<br />
• \phi component
  <br /> \frac{J}{r^2 \sin(\theta)^2} = E \; \frac{\tilde{J}}{r^2 \sin(\theta)^2}<br />

Then put \theta=\pi/2 because we are interested in taking the inner product at an event lying in the equatorial plane, which gives (on the equatorial plane, and grouping the two angular components):
<br /> \vec{k} &amp; = &amp; E \; \left( \frac{1}{1-2m/r} \, \partial_t <br /> - \sqrt{1-\tilde{V}} \, \partial_r<br /> + \frac{1}{r^2} \; \left( \sqrt{\tilde{L}^2-\tilde{J}^2} \, \partial_\theta <br /> + \tilde{J} \, \partial_\phi \right) \right)<br />
Then observe that the coordinate derivatives dr/dt, \, d\theta/dt, \, d\phi/dt determine the "shape" of the curve and only depend on \tilde{L}, \, \tilde{J}. (Darn it, VBulletin is hiding the tildes over those letters, which completely munges my notation!) In particular, the impact parameter depends only on the total specific angular momentum \tilde{L}.

 

[DrGreg]

(Darn it, VBulletin is hiding the tildes over those letters, which completely munges my notation!)

There seems to be a bug in the LaTeX which shaves the top row of pixels off an ITEX image. The fix is to use a TEX image instead.

 

[Chris Hillman]

Yes, the problem seems to be that it tries to "raise" the baseline, so that the top is sheared off. Thus, the bug applies to overhat, tilde, sometimes even overbar.

(In case anyone is wondering, yes, I saw the internationally reported news stories on another recent security flaw with at least one version of VBulletin, but that should be discussed in SA forum, and probably only after getting permission from a Mentor.)

 

[Chris Hillman]

BRS: Computing optical experience. Ib. Overview

In my first attempt, I now think I was rushing much too fast to get to the "good stuff" (black holes), so let me try to start over.

I. Overview

Some 15-20 years ago, I recall asking Andrew Hamilton (Univ. of Colorado, author of a fine expository website, and more recently, eprints on the "river picture" for Schwarzschild holes), by email, why there was no lavishly produced IMAX film depicting infall into a black hole. As I recall, he replied that such projects were in the works, but apparently they never came to fruition. Given the intense continuing public interest in black holes, it remains mysterious to me why no film has been produced depicting accurately the optical experience of an observer approaching, orbiting or falling inside a (stellar mass, or supermassive) black hole according to various scenarios, showing for example a generous sampling of genuine stars/galaxies in true color with relavistic ray-tracing and with all gtr frequency shifts taken into account, and perhaps also depicting views of probes falling into the hole, or of a companion star and accretion disk orbiting the hole.

Be this as it may, SA/Ms who participate in the astrophysics, cosmology, and relativity subforums at PF have no doubt noticed that the subject of frequency shift comes up very often, perhaps because this is one of the few topics within the technical grasp of the average beginning student--- as long as one confines oneself to the simplest scenarios, such as light from "the distant fixed stars" as received by a static or infalling observer near a Schwarzschild object (modeling a massive nonrotating isolated object, i.e. providing a particularly simple idealized model of the gravitational field of a black hole or of a star).

In addition, the propagation of information via massless radiation of various kinds (e.g. EM radiation, gravitational radiation, ?) is a fundamental phenomenon in physics. In classical physics, such radiation plays a fundamental role in explaining how events "there and then" can effect "here and now" due to "field updating information" propagating via massless radiation. In the "geometric optics limit", modeling the propagation of massless radiation is largely reduced to the behavior of null geodesics in a four-dimensional Lorentzian manifold. When this manifold is curved, everything is greatly complicated, but even models set in Minkowski spacetime can present technical challenges.

In this thread, I'd like to try sketch a unified approach which in principle applies quite generally, although in practice (as almost always happens in the study of exact solutions in gtr), various symmetry assumptions prove to be very helpful, even essential for actually carrying out the program.

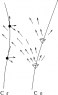
The bare bones of the situation I plan to study consists of

• two given world lines (timelike curves, not neccessarily geodesics) C_e, C_r
• one or more null geodesics from C_e (the world line of the emitter) to C_r (the world line of the receiver)

At the very least, we will need to know how to compute, for each null geodesic path from C_e to C_r

• the ratio of energy measured at C_e to energy measured at C_r, i.e. the frequency shift as measured by our observer
• the direction from which the signal arrives at C_r (wrt a frame field defined along C_r)

See the figure below.

But to compute an IMAX movie of the optical experience of an observer (with world line C_e), even in the simplest case where the only "objects in view" are distant pointlike stars, we will need more. We must define the world lines of each pointlike luminous object in the scene, we will need to model the various signals propagate to C_r, and we will need to provide C_r with a nonrotating frame field with we can use to describe the optical experience of our observer.

Then we hope to compute, as a function of the proper time of our observer, a plot of the apparent motion of the various sources on the celestial sphere of our observer, which is tied to the three spatial vectors of the frame. The scene can be plotted on a computer screen using stereographic projection, which is a conformal (angle preserving) mapping of S^2 to E^2 which preserves the size and shape of "small images"; we can think of it as a mathematically convenient "fish eye lens".

When we come to specific examples, it will become clear, I think, that even in Minkowski vacuum, expressing specific world lines as proper time parameterized timelike curves, or expressing specific signal paths as affinely parameterized null geodesic curves, can be difficult. Fortunately, it is much, much easier to determine and work with the timelike or null vector fields (respectively) whose integral curves yield the desired world lines or signal paths (respectively).

We can probably not avoid the need to find at least the world line of the observer, but another simplification is possible with respect to the world lines of the emitters: as so often happens in mathematics, taking a limit can simplify expressions greatly, and in practice, in the kind of asympotically flat spacetime models we are ultimately interested in, it can be very useful to take advantage of such simplication.

For each emitter world line C_e, we want to avoid actually finding the signal paths. The next idea is to defined and employ a special null geodesic congruence, the so-called beacon congruence, which consists of all future directed null geodesics issuing from C_e. These geodesics are to be affinely parameterized. The wave vector field (tangent vectors defined by the geodesics) \vec{k} is then our principle tool in studying the propagation of information from events on C_e; see figure below.

You probably see where this going: we have a frame attached to our observer's world line C_r, and it is often convenient to choose a frame field defining our spacetime model M in which C_r is one integral curve of the timelike unit vector field \vec{e}_1 in our frame field. Then the inner product
<br /> -\vec{e}_1 \cdot \vec{k}<br />
will enable us to compute the frequency shift, if any, for a given signal as received at C_r. Furthermore, the inner products with the spacelike unit vectors
<br /> b_2 = \vec{e}_2 \cdot \vec{k}, <br /> \; \; b_3 = \vec{e}_3 \cdot \vec{k},<br /> \; \; b_4 = \vec{e}_4 \cdot \vec{k}<br />
give the components of the momentum of the "photon" wrt the frame at C_r. The result will be expressions containing the coordinates and any parameters used in defining the world lines of the emitter and receiver, as well as any parameters used in defining the spacetime itself. We need to convert this information into appropriate functions of proper time along the world line C_r. We can accomplish that by computing C_r as a proper time parameterized geodesic, which means we give the four coordinates as differentiable functions of the proper time parameter (usually written s), and then plugging these in for the coordinates.

Next, we need to further process our results to obtain a plot on the celestial sphere of our observer. But this is straightforward if we use stereographic projection at each event along C_r, where we can adopt the convention that the N, S poles of the celestial sphere will be identified with
<br /> \pm \vec{e}_4<br />
while
<br /> \cos(\psi) \, \vec{e}_2 + \sin(\psi) \, \vec{e}_3<br />
traces out the equator (this should be understood as an expression defined on the tangent space to an event on C_r). The result is the apparent position of the signal source plotted on the celestial sphere as a function of proper time
<br /> \vec{n} = - \, \frac{ b_2 \, \vec{e}_2 + b_3 \, \vec{e}_3 + b_4 \, \vec{e}_4 }<br /> {\sqrt{b_2^2 + b_3^2 + b_4^2}}<br />
(where b_2, b_3, b_4 are now known as functions of the proper time kept by our observer). Because Maple (and Mathematica, as I recall) enable the user to colorize curves using any function, we can ensure that each point on this curve (plotted on S^2 and mapped to E^2 by stereographic projection) is given the appropriately frequency shifted color.

Maple (and Mathematica, as I recall) are equipped with useful animation functions which allow one to plot frames from a "movie" and then run them forward or backward in "time" using a slider, so we can also compute animated simulations for as many sources as we like, assuming we are prepared to compute the appropriate beacon congruence for each source.

I should stress here that while this program applies in principle quite generally, in practice finding the beacon congruences can be hard (although much easier than finding null geodesics as parameterized curves), and we still need to find the world lines of the receiver and the emitters as parameterized curves. But as already mentioned, we can expect to greatly simplify our computations by moving most or all of the emitters "to spatial infinity", in the case where M is asymptotically flat.

In the next post, I plan to illustrate how this process works in Minkowski spacetime, using receivers and emitters exhibiting various types of simple motion:

• inertial motion (world line a straight line)
• uniform path curvature/acceleration (world line a hyperbola)
• centripetal motion (world line a helix in spacetime)

In the third post (perhaps) I could show how much of this carries over to the simplest cosmological model, FRW dusts with E^3 hyperslices orthogonal to the world lines of the dust particles. In the fourth post (perhaps) I could discuss Schwarzschild vacuum. (With this in hand, generalization to Reissner-Nordstrom-de Sitter electrolambdavacuum is not terribly hard; generalization to Kerr vacuum is a bit harder but also feasible.) In the fifth post (perhaps) I could discuss how we can take advantage of conformal compactification to streamline the treatment of emitters at r=infinity by considering a beacon congruence defined by some curve on past null infinity. Scenarios set in a pp-wave spacetime are also of considerable interest.

Figures (left to right):

• Two world lines, C_e, C_r and one or more null geodesics (dotted) from an emission event on C_e to reception events on C_r; note the frame attached to C_r
• The null vector field whose integral curves define the beacon congruence (all future directed null geodesics issuing from C_e), and a frame defined along C_r