Calculate Heating Time for Water Bath to Reach 58.9°C

  • Thread starter Thread starter Heart
  • Start date Start date
  • Tags Tags
    Heating Water
AI Thread Summary
To calculate the heating time for water to reach 58.9°C from 10.1°C using a 20-ohm resistor, the energy required is approximately 20,856.144 J. The initial calculations incorrectly considered the total resistance of 30 ohms instead of just the 20-ohm resistor in the water bath. The correct approach involves using the power output from the 20-ohm resistor, applying the formula P = I²R to find the current and power. The misunderstanding arose from the relationship between resistance and power output, where less resistance leads to longer heating times when considering the effective current. The final calculations confirmed the correct heating time, clarifying the importance of focusing on the specific resistor in the water.
Heart
Messages
39
Reaction score
0
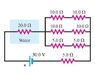
"In the circuit in the figure, a 20-ohm resistor sits inside 102 g of pure water that is surrounded by insulating Styrofoam."

"If the water is initially at temperature 10.1 deg. celsius, how long will it take for its temperature to rise to 58.9 deg. celsius?
Use as the heat capacity of water, and express your answer in seconds using three significant figures."

What I did was finding the total resistance to be equal to 30 ohms.

I then use the mc(delta t) formula; the energy needed is then equal to 20856.144 J. I then equated this to P=V^2/R. I then found the time to be ~ 656 seconds. I'm pretty sure I did it right but MP said I did it wrong. Any suggestions?

Thanks in advance,
 

Attachments

  • water bath.jpg
    water bath.jpg
    10.7 KB · Views: 681
Physics news on Phys.org
I found P to be 30 J/s; V is given = 30 volt and total R was found to be 30 ohms. I thought I got it wrong cos of using 30 ohms so I tried using 20 ohms (resistance of the resistor in the water bath) instead of the resistance of the total systemk, but I still got it wrong. Any suggestions? Please help. :cry:
 
You're calculating the required heat energy to raise the temperature of the water correctly.

The mistake you are making is in taking the total resistance of the circuit. Remember only the 20 ohm resistor is in the water, so you only want the power output from that one. Try calculating the current through that resistor and applying P = I^2R. Here R should be the 20 ohm resistance only.
 
Last edited:
Thanks for the tip. I got the answer now. It didn't make sense to me though on why it'd take longer to heat when there're less resistors.
 
Heart said:
Thanks for the tip. I got the answer now. It didn't make sense to me though on why it'd take longer to heat when there're less resistors.

Because you're only considering the power output from the 20 ohm resistor rather than from the whole 30 ohm resistance in the circuit. The current through the single 20 ohm resistance is equal to that through the "effective" 10 ohm resistance formed by the remaining resistors (since they're in series). When the current is the same, the power output is directly proportional to the resistance. Do you see now ?
 
Thanks, I do now. :)
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Specific heat capacity and latent heat
Replies
2
Views
248
I try to solve a thermodynamics problem on heat transfer
Replies
3
Views
2K
Cylinder in a heat bath @ 0C contains water and ice & is compressed
Replies
19
Views
2K
Confusion about whether to use the specific heat of water or ice
Replies
4
Views
2K
Calorimetry - finding the final temperature of a system of ice and water
Replies
7
Views
2K
Thermodynamics -- Calculations for heating water up
Replies
2
Views
1K
Experimenting whether the diameter of a pot affects boiling time for water
Replies
15
Views
2K
Calculate the Heat Loss in a Hot Water Tank from a Shower
Replies
2
Views
3K
Finding the Initial Temperature of Water in a Calorimeter: A Calorimetry Problem
Replies
2
Views
3K
How Does a Resistor Affect the Heating Time of Water?
Replies
6
Views
3K

Hot Threads

Recent Insights

Back
Top