Calculate how much the light has been displaced

[mimi.janson]

Homework Statement

hello i have a question i really don't get how to solve

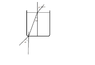
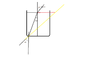
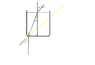
a laserlight with the wavelength of 630 goes from air to glas of water with the angle of incidence = 40 degrees. The glass is 10 cm

I have to calculate how much the light has been displaced in the water when it goes out to the air again after the 10 cm

please i ned a step by step on how to solve it

I have solved that the angle of refraction is 28,9 degrees

Homework Equations

I have put a photo of it so u can see what i mean,

The Attempt at a Solution

all the numbers in photo there i have calculated so maybe they arent right but i did it as good as I am able to...they ask me how much will the light be displaced when it gets back to air again (and to be honest i don't get the question too well but i guess it is something about how it will be when it goes out to the air from the bottom of the glass)

 

[mimi.janson]

how come no one is helping me ?

 

[davo789]

Because it's a fairly new post and you haven't made a clear effort to solve the problem?

 

[mimi.janson]

Because it's a fairly new post and you haven't made a clear effort to solve the problem?

i have been trying to solve it for 3 hours now because i normally try before asking ? i now that when the light is displaced in the water and goes back out in the air you go back to the original angle but i just don't understand what they want me to do in the question ? as u see i have drawn what i think it is on the attached photo, but i just don't get what they mean i have to find on the photo

 

[davo789]

How did you calculate the angle of refraction?

 

[mimi.janson]

How did you calculate the angle of refraction?

the angle where i have written 40 degress was given so i just had to solve one which i remember the formula for

I know that when u go from air to water then:
(Sin(i))/(Sin(b))=(3,00*〖10〗^8 m/s )/(2,25*〖10〗^8 m/s)=1,33

then there is a physics law that says

(Sin(40))/(Sin(b))=1,33
Sin(b)=(Sin(40))/1,33=0,48329
and since i have to find the degress of the angle i have to use sin-1
〖Sin〗^(-1)=28,9
b=28,9°

 

[davo789]

OK great. The 'displacement' is the distance between the incoming and outgoing beam if you were to lie them next to each other.

Draw on your diagram a few lines to see if you can make sense of what's going on. A good hint is that you will need to calculate the distance the light travels in the water.

 

[mimi.janson]

so do you think my calculation of the angle of refraction is ok ?

but when they ask how much the light will have been displaced after coming out in the air again i don't get it...because as you see on the photo i have made it is clearly that it goes back to being 40 degress again which means that it goes back to not being displaced...but then again i have thought that they maybe want me to draw an line as long if it was only in air and then measure the difference but i don't understand which i should do and maybe both are wrong


but the incoming and outgoing are both 40 because it goes back to the old state when geoing back to air ? or am i wrong

 

[davo789]

No your drawing is correct. But, let's assume the incoming beam is the bottom one. It goes in, and is 'jogged' to the left by the water. When it comes out, it is heading in the same direction but is displaced to the left by a little.

 

[davo789]

And yes, your calculation of the refraction angle is also correct.

 

[mimi.janson]

if i have to calculate it then i think it is because i now know that i have a angle 28,9 and one 90 degrees and then i have the 10 cm so i have to use tan

10 cm*tan28,9 = 5,5 ? but this isn't right when u look at the picture i put in because it should even become longer than the 10 cm since it goes across

 

[davo789]

You're right in saying that it should get longer. Why do you think that you've got to use tan?

 

[mimi.janson]

No your drawing is correct. But, let's assume the incoming beam is the bottom one. It goes in, and is 'jogged' to the left by the water. When it comes out, it is heading in the same direction but is displaced to the left by a little.

now that u put it that way and i look at it from the bottom insted from the top i think i can actually see what are referring to.

please would u check the new photo i just posted ? i did put some new lines because i come to think of what if i just thought of the water as air and kept it on 40 degrees and then later measured the red distance ? but on the other hand it would be hard to know how long the yellow should be

 

[mimi.janson]

You're right in saying that it should get longer. Why do you think that you've got to use tan?

well u said that i had to know how long it was in the water and since i know about two degrees which were 28,9 and the 90 and only one length which was the 10 cm then i thought it had to be tan


DAVO I JUST ANSWERED U TWO TIMES BUT IT IS ON THE NEXT PAGE SINCE THE WASN'T ENOUGTH PLACE HERE ...U CAN CLICK NEXT PAGE AT THE BOTTOM

 

[davo789]

The yellow line is correct but the red one isn't. The distance you want is a line between the beams that is perpendicular (at right-angles) to them.

 

[davo789]

well u said that i had to know how long it was in the water and since i know about two degrees which were 28,9 and the 90 and only one length which was the 10 cm then i thought it had to be tan

It would really help if you could update your drawing with the lines etc. that you are referring to. If you label each line a,b,c etc. and the angles with greek letters then it will make things much easier :)

 

[mimi.janson]

The yellow line is correct but the red one isn't. The distance you want is (at right-angles)a line between the beams that is perpendicular (at right-angles) to them.

"a line between the beams that is perpendicular (at right-angles) to them. "

sorry i don't get that part of your sentence could u please say it in some other way ...its because i don't understand the words perpendicular, right-angles(here i think of the right like right hand u write with and angle i know what angle is) but i don't get the line in a whole

 

[mimi.janson]

It would really help if you could update your drawing with the lines etc. that you are referring to. If you label each line a,b,c etc. and the angles with greek letters then it will make things much easier :)

well yeah i guess i know what u mean now i see I am just talking in my own thought, but here comes an update again

the square on A means 90 degress and my B is the 28,9 i found earlier, and i know that the length from A to B the stright line is 10 cm

so i thought i could use these informations to find the length of the green line

 

[davo789]

"a line between the beams that is perpendicular (at right-angles) to them. "

sorry i don't get that part of your sentence could u please say it in some other way ...its because i don't understand the words perpendicular, right-angles(here i think of the right like right hand u write with and angle i know what angle is) but i don't get the line in a whole

All you need to do is rotate your red line until it is at 90 degrees to the yellow (and thus also the outgoing) beam. That is the length you are trying to find.

 

[davo789]

well yeah i guess i know what u mean now i see I am just talking in my own thought, but here comes an update again

the square on A means 90 degress and my B is the 28,9 i found earlier, and i know that the length from A to B the stright line is 10 cm

so i thought i could use these informations to find the length of the green line

You can indeed use this info to find the length of the green line. And you have also drawn the triangle correctly. Look at it again to see if you can which trig function to use (remember 'SOH CAH TOA' if it helps).

 

[mimi.janson]

ok i found it :) thanks alot