Pivskid
- 8
- 0
I have a construction of a vibrator (industrial use).
I should be able to calculate the natural frequency, by means of Hooke's law.
Since I have a physical device I already have a "real world" measurement of the Natural frequency.
The problem is: How to calculate it?
I have tried to do some equivalent work, and a calculation that is far of the measured value.
You could say "why calculate when you have the measured value".
The vibrator at hand now, is only a model.
I need to be able to calculate the NF fairly accurate, in order not to demolise the building where the real one is installed )
)
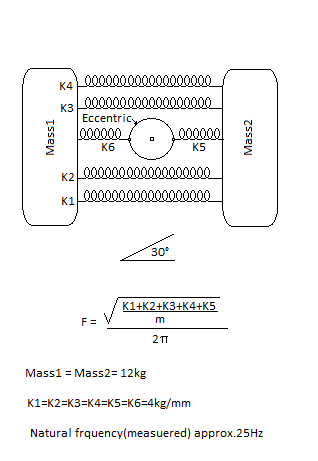
Observe that the 2 mass'es are placed in an angle of 30° from horizontal.
That is..mass2 is higher than mass1.
All springs are equal, eventhough the drawing might insinuate otherwise.
I should be able to calculate the natural frequency, by means of Hooke's law.
Since I have a physical device I already have a "real world" measurement of the Natural frequency.
The problem is: How to calculate it?
I have tried to do some equivalent work, and a calculation that is far of the measured value.
You could say "why calculate when you have the measured value".
The vibrator at hand now, is only a model.
I need to be able to calculate the NF fairly accurate, in order not to demolise the building where the real one is installed
Observe that the 2 mass'es are placed in an angle of 30° from horizontal.
That is..mass2 is higher than mass1.
All springs are equal, eventhough the drawing might insinuate otherwise.
Last edited: