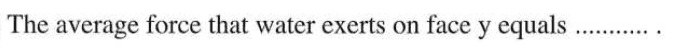SUMMARY
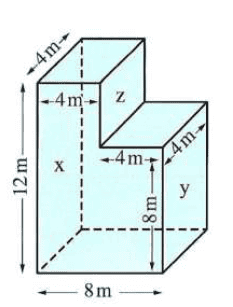
The discussion centers on calculating the average force on the side walls of a container filled with fluid, specifically addressing the pressure exerted by the fluid at different heights. The correct formula for the force on the side wall is established as F = ρg(h_z)A_y, where ρ is the fluid density, g is the acceleration due to gravity, h_z is the height of the fluid column above the point of interest, and A_y is the area of the side wall. Participants clarify that pressure in a fluid acts equally in all directions and that the pressure at a depth h is given by ρgh, which varies from the top to the bottom of the wall.
PREREQUISITES
- Understanding of fluid mechanics principles, specifically hydrostatic pressure.
- Knowledge of the concepts of pressure and force in fluids.
- Familiarity with the variables involved in fluid dynamics equations, such as density (ρ) and gravitational acceleration (g).
- Basic integration techniques for calculating forces over varying pressure distributions.
NEXT STEPS
- Study the derivation of hydrostatic pressure equations in fluid mechanics.
- Learn about the application of integration in calculating forces on surfaces submerged in fluids.
- Explore the implications of varying fluid density on pressure calculations.
- Investigate real-world applications of fluid pressure calculations in engineering and design.
USEFUL FOR
Students and professionals in engineering, particularly those specializing in fluid mechanics, civil engineers involved in design and analysis of fluid containers, and anyone interested in understanding the principles of pressure and force in fluids.