Calculate the current through each ideal battery

[perfect_piccolo]

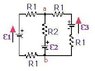
1. (a) Calculate the current through each ideal battery in the figure. Assume that R1 = 1.0 Ω, R2 = 2.0 Ω, ε1 = 4.0 V, and ε2 = ε3 = 8.0 V. Take positive current as that flowing through the battery from - to +. (See diagram)




I just need some guidance about how to set this problem up.

I've tried applying the Junction rule, to give me I1 + I3 = I2

And then the Loop rule to give:

4.0 V - 1(I1) - 2(I2) - 8V - 1(I1) = 0

8V - 1(I3) - 2(I2) - 8V - 1(I3) = 0



Am I setting this problem up correctly and using the right equations?

Thanks

 

[kamerling]

According to the problem, you should have taken I2 in the other direction. Either replace I2 by -I2 in all equations, or replace I2 by -I2 after you're done. Apart from that it's ok.

 

[Moetasim]

for your question. The approach you have taken is a good start, but there are a few things that need to be corrected in order to solve the problem correctly.

First, let's look at the junction rule. You are correct in using it to express the relationship between the currents at the junction point. However, it is important to note that the direction of the currents should be taken into account. In this case, the current I1 is flowing into the junction from the left, while I2 and I3 are both flowing out of the junction. This means that the correct expression for the junction rule would be: I1 = I2 + I3.

Next, let's look at the loop rule. This rule states that the sum of the voltage drops around a closed loop in a circuit must equal the sum of the voltage sources. In this problem, there are two loops - one containing R1 and the 4.0V battery, and one containing R2 and the two 8.0V batteries. Using the loop rule for the first loop, we get: 4.0V - 1(I1) - 1(R1) = 0. Similarly, for the second loop, we get: 8.0V + 2(I2) - 2(R2) - 8.0V = 0.

Now, we have two equations and three unknowns (I1, I2, and I3). We can solve for one of the currents using the junction rule, and then substitute that value into one of the loop rule equations to solve for the remaining currents.

Using the junction rule, we can express I1 in terms of I2 and I3 as: I1 = I2 + I3. Substituting this into the first loop rule equation, we get: 4.0V - (I2 + I3) - 1(R1) = 0. Simplifying, we get: 4.0V - I2 - I3 - 1.0V = 0. Similarly, for the second loop rule equation, we get: 8.0V + 2(I2) - 2(R2) - 8.0V = 0. Simplifying, we get: 2(I2) - 2.0Ω - 8.0V = 0.

Now, we have two equations and two unknowns (