Calculate the discriminant of a basis [Number Theory]

[Firepanda]

Question:

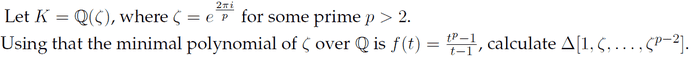
The needed proposition and two examples:

This is as far as I have got:

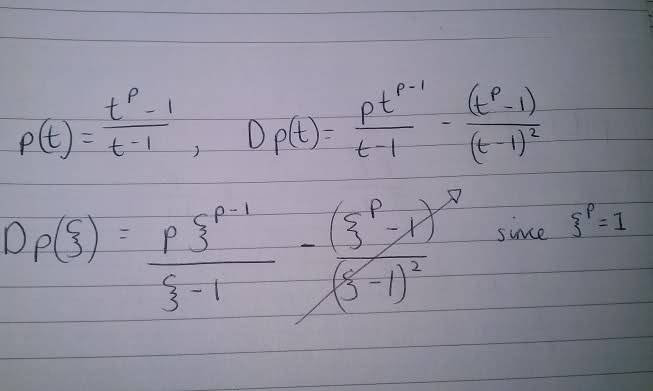
I need to reduce this (I think) so I can represent is as a matrix! Any idea on how to do this?

Thanks

 

[morphism]

How about rewriting your last equation as
(\zeta - 1)Dp(\zeta) = p\zeta^{p-1} and then taking norms of both sides?

 

[Firepanda]

I'm unsure on how to calculate N(p\zeta^{p-1})

N(\zeta - 1) = 5 though.

 

[morphism]

N(\zeta - 1) isn't 5 - not unless p=5.

As for N(p \zeta^{p-1}), this is just N(p)N(\zeta)^{p-1}, and N(p) and N(\zeta) are really easy to compute.

 

[Firepanda]

Providing N(\zeta - 1)=p (is this easy to prove?) then I also get N(p)=p^{2} and N(\zeta)=1

So my overall answer should be p?

 

[morphism]

N(p) should be p^{p-1}.

And as for computing N(\zeta-1), you can either do it the determinant way (and do a bunch of row operations), or you could use the differentiation trick you used above except with t=1 isntead of t=\zeta.

 

[Firepanda]

Hmm when t=1 I get the denominator as 0, am I not using it right?

 

[morphism]

Notice that
t^p - 1 = (t-1)(t-\zeta)\cdots(t-\zeta^{p-1}) so the t-1 in the denominator gets canceled off.

Edit:
Actually, we don't want to be looking at (t^p-1)/(t-1), rather just at t^p-1. Differentiate both sides of the equation above and plug in t=1.

 

[Firepanda]

Just to be clear you want me to differentiate both sides of t^p - 1 = (t-1)(t-\zeta)\cdots(t-\zeta^{p-1})?

Unsure on how to do the RHS without getting messy!

 

[morphism]

Yes, that's what I want you to differentiate. It won't be too messy (especially if you plug in t=1 after you differentiate). :)

 

[Firepanda]

Hmm I'll admit I'm not sure how to go about doing the RHS!

Do I need to? Why can't I use just the differential of the LHS?

 

[morphism]

If you differentiate the RHS and plug in t=1, everything will immediately vanish except for the first term, which becomes
(1-\zeta)(1-\zeta^2)\cdots(1-\zeta^{p-1}).
This really just follows from the product rule of differentiation.

 

[Firepanda]

If you differentiate the RHS and plug in t=1, everything will immediately vanish except for the first term, which becomes
(1-\zeta)(1-\zeta^2)\cdots(1-\zeta^{p-1}).
This really just follows from the product rule of differentiation.

Ah I see, sorry I've never used the product rule for more than 2 terms before, I get it now!

so p = (1-\zeta)(1-\zeta^2)\cdots(1-\zeta^{p-1})

i suppose we want to rearrange this?

 

[morphism]

No real rearrangement is necessary. Just notice that the RHS is also (\zeta - 1)(\zeta^2 - 1) \cdots (\zeta^{p-1}-1) (because p is odd), which is just the product of all the conjugates of \zeta-1, a.k.a. _____

 

[Firepanda]

Norm!

So the norm is p? Havn't we got a few too many conjugates though?

 

[morphism]

Yes, the norm is p, and no we have the right amount of conjugates! This is because the conjugates of \zeta are \zeta itself and \zeta^2, \ldots, \zeta^{p-1}. Try to actually write down a rigorous proof, using minimal polynomials. It should be easy.

 

[Firepanda]

Ok thanks :)

Is N(p) = p^p-1 since we can write the matrix as a matrix with only p along the diagonal?

 

[morphism]

Ok thanks :)

Is N(p) = p^p-1 since we can write the matrix as a matrix with only p along the diagonal?

Yup!