physicslover14
- 16
- 0
Homework Statement
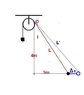
Consider the following arrangement
Calculate the work done by tension on 2kg block during its motion on circular track from point A to point B.
Homework Equations
The Attempt at a Solution
We know that work done by a force is product of force and displacement.
We know the displacement of point of application as 4 m. How to find the work done by the tension as it is not constant it is variable.
Attachments
Last edited: