Calculating a matrix element & first order shift

[StephvsEinst]

So I saw this a moment ago:

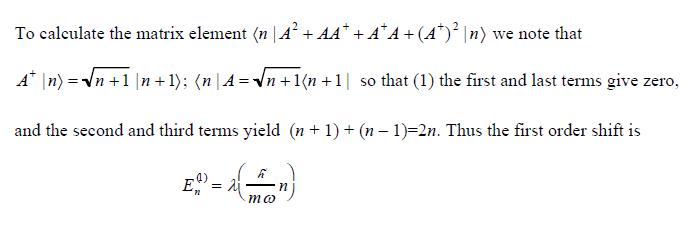
How can the second and third terms yield (n+1)+(n-1)=2n and not (n+1)+n=2n+1?
PS: I solved the problem by using [a,a(+)]=1.

Sorry, this is very simple but I cannot figure out what I did wrong.

 

[dextercioby]

It's not clear to me what A|n> is equal to. This is very important, since (dropping the finesse of domain issues linked to unbounded operators on Hilbert space)

$$\langle n, A^{\dagger} A n\rangle = \langle A^{\dagger\dagger} n, A n\rangle = \langle A n, A n\rangle$$

$$\langle n, A A^{\dagger} n\rangle = \langle A^{\dagger} n, A^{\dagger} n\rangle = \sqrt{n+1}^2 = n+1$$

 

[StephvsEinst]

Thank you, I understood your answer: simple and pratical.
Here, A|n> is equal to sqrt(n)|n-1> and A(+)|n> is equal to sqrt(n+1)|n+1>.

PS: Sorry for not using the math font but I am too lazy right now to insert it in latex.