Calculating circle chords for lumber template

[DaveC426913]

I am building a custom arbour with a semi-circular arch. I wish to calculate how much of an arc I can get out of a given width of lumber.

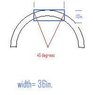
My arch has a 45" inner diameter and is 3 1/2" thick (same thickness as the 4x4 uprights it will sit on) for an outer diameter of 52".

If I start with a 2"x10" piece of lumber, it is possible to get a full 90 degree arc out of it. This uses up 36" of wood.

But what if I used a 2"x8" piece of lumber? Could I get a smaller degree arc out of that? How long would the lumber have to be? Conversely, what is the maximum angle of arc I could get out of a 2x8?

Ultimately, I want to optimize the cost of the arch.
2x10 is 1.89/ft,
2x8 is 1.23/ft.

 

[HallsofIvy]

Basically, you have two isosceles triangles, sharing a single vertex, and want to find the distance between the two bases. With outer diameter 52" and thickness 3 and 1/2 ", you have isosceles triangles with side length 52- 3.5= 48.5" and 52". Dropping a perpendicular to the center of the two bases gives two right triangles with angle 15 degrees and hypotenuses of length 48.5 and 52. The "near sides" of the two triangles are 48.6 cos(15)= 46.847 and 52 cos(15)= 50.228 and the thickness of board you will need is 50.228- 46.847= 1.38" which is well within your board. The length of board you will need is the length of the base of the larger isosceles triangle, twice the length of the opposite side of the larger right triangle, 2(52)sin(15)= 26.9 inches.

 

[DaveC426913]

Well, I've never been good at checking my numbers so instead, I mapped it out at 1:1 on some newspaper.

A 90 degree arc will fit on a 2"x10" plank in 36".
A 45 degree arc will fit on a 2"x6" plank in only 19.5".

Hm. 2x6's will be cheaper than 2x10's, but 4x45 joints will be weaker than 2x90 joints...

 

[DaveC426913]

Basically, you have two isosceles triangles, sharing a single vertex, and want to find the distance between the two bases. With outer diameter 52" and thickness 3 and 1/2 ", you have isosceles triangles with side length 52- 3.5= 48.5" and 52". Dropping a perpendicular to the center of the two bases gives two right triangles with angle 15 degrees and hypotenuses of length 48.5 and 52. The "near sides" of the two triangles are 48.6 cos(15)= 46.847 and 52 cos(15)= 50.228 and the thickness of board you will need is 50.228- 46.847= 1.38" which is well within your board. The length of board you will need is the length of the base of the larger isosceles triangle, twice the length of the opposite side of the larger right triangle, 2(52)sin(15)= 26.9 inches.

Are you accounting for the full width of the arc? It seems to me, those two triangles do not, but I may be misunderstanding you.

See diagram.

 

[CarlAK]

Using CAD rather than math..
I get that with a 10" plank (9.5" actual) you do not quite get 90 degrees, you get 86 degrees out of a 35.3" length.
For a n 8"/7.5", you can get 70 degrees from 29.6"
for a 6"/5.5", you can get 48 degrees from 21.4", or 45 degrees from 19.9"

Does this help? I assume you'd want to use 2-45 degree pieces rather than 70 & 20 or something like that. So maybe the comparison should be 2 ea 19.9" 2x6; versus 35.3" 2x10 (but which is less than 90 degrees).