- #1
scriptymender
- 4
- 0
G'day guys,
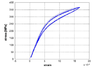
I am currently trying to calculate the damping ratio for Shape memory alloys using hysteresis loops. The damping ratio is usually represented as ΔU/2∏U, where ΔU is the energy lost due to material damping and U is the elastic strain energy. My problem is trying to find this elastic strain energy due to the unusual behaviour of shape memory alloys. I have attached an example of a hysteresis loop for an SMA undergoing the super elastic effect. If anyone could give me any help or guidance I would be extremely grateful and may even buy you a beer!
Thanks, Leon
I am currently trying to calculate the damping ratio for Shape memory alloys using hysteresis loops. The damping ratio is usually represented as ΔU/2∏U, where ΔU is the energy lost due to material damping and U is the elastic strain energy. My problem is trying to find this elastic strain energy due to the unusual behaviour of shape memory alloys. I have attached an example of a hysteresis loop for an SMA undergoing the super elastic effect. If anyone could give me any help or guidance I would be extremely grateful and may even buy you a beer!
Thanks, Leon